题目内容
1. 如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1P2交OA于M,交OB于N.若∠AOB=30°,则∠P1OP2=60°.
如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1P2交OA于M,交OB于N.若∠AOB=30°,则∠P1OP2=60°.
分析 根据轴对称的性质,∠AOB=30°,P为∠AOB内部一点,点P关于OA、OB的对称点分别为P1、P2,∠AOP=∠AOP1,∠BOP=∠BOP2,可求出∠P1OP2的度数.
解答 解:∵P1与P关于OA对称,
∴OP=OP1,
∵P2与P关于OB对称,
∴OP=OP2,
∴OP1=OP2,
∵P1与P关于OA对称,
∴∠POA=∠AOP1,
∵P2与P关于OB对称,
∴∠BOP=∠BOP2,
又∵∠P1OP2=∠AOP1+∠AOP+∠BOP+∠BOP2,
∵∠P1OP2=∠BOP+∠BOP+∠AOP+∠AOP,
=2(∠BOP+∠APO),
=2∠AOB,
∵∠AOB=30°,
∴∠P1OP2=2×30°=60°.
故答案为:60°.
点评 本题考查了轴对称的性质,即对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
相关题目
12.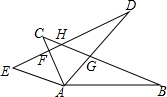 如图,AB=AD,AC=AE,∠BAD=∠CAE,现在有下列结论:①DE=BC;②AC⊥DE;③∠CAE=∠DHG;④S△ABG=S△AEF+S△DGH;⑤AF=AG,其中正确的结论个数为( )
如图,AB=AD,AC=AE,∠BAD=∠CAE,现在有下列结论:①DE=BC;②AC⊥DE;③∠CAE=∠DHG;④S△ABG=S△AEF+S△DGH;⑤AF=AG,其中正确的结论个数为( )
 如图,AB=AD,AC=AE,∠BAD=∠CAE,现在有下列结论:①DE=BC;②AC⊥DE;③∠CAE=∠DHG;④S△ABG=S△AEF+S△DGH;⑤AF=AG,其中正确的结论个数为( )
如图,AB=AD,AC=AE,∠BAD=∠CAE,现在有下列结论:①DE=BC;②AC⊥DE;③∠CAE=∠DHG;④S△ABG=S△AEF+S△DGH;⑤AF=AG,其中正确的结论个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9.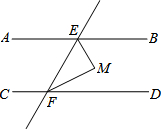 如图,直线AB∥CD,EF分别交AB、CD于点E、F,EM平分∠BEF,FM平分∠DFE,则∠EMF的度数为( )
如图,直线AB∥CD,EF分别交AB、CD于点E、F,EM平分∠BEF,FM平分∠DFE,则∠EMF的度数为( )
 如图,直线AB∥CD,EF分别交AB、CD于点E、F,EM平分∠BEF,FM平分∠DFE,则∠EMF的度数为( )
如图,直线AB∥CD,EF分别交AB、CD于点E、F,EM平分∠BEF,FM平分∠DFE,则∠EMF的度数为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
16. 如图,在?ABCD中,AC、BD相交于O,F在BC延长线上,交CD于E,如果OE=EF,则BF:CF等于( )
如图,在?ABCD中,AC、BD相交于O,F在BC延长线上,交CD于E,如果OE=EF,则BF:CF等于( )
 如图,在?ABCD中,AC、BD相交于O,F在BC延长线上,交CD于E,如果OE=EF,则BF:CF等于( )
如图,在?ABCD中,AC、BD相交于O,F在BC延长线上,交CD于E,如果OE=EF,则BF:CF等于( )| A. | 3:1 | B. | 2:1 | C. | 5:2 | D. | 3:2 |
6.下列四个式子中,是方程的是( )
| A. | 2x-6 | B. | 2x+y=5 | C. | -3+1=-2 | D. | $\frac{4}{6}$=$\frac{2}{3}$ |
13.超市出售的三种品牌月饼袋上,分别标有质量为(300±5)g,(300±10)g,(300±15)g的字样,从中任意拿出两袋,它们的质量最多相差( )
| A. | 10g | B. | 20g | C. | 30g | D. | 40g |
11. 将正整数按如图所示的位詈顺序排列:根据排列规律,则2016应在( )
将正整数按如图所示的位詈顺序排列:根据排列规律,则2016应在( )
 将正整数按如图所示的位詈顺序排列:根据排列规律,则2016应在( )
将正整数按如图所示的位詈顺序排列:根据排列规律,则2016应在( )| A. | A位置 | B. | B位置 | C. | C位置 | D. | D位置 |
 我国古代的《河图》是由3×3的方格构成,每个方格均有数目不同的点图,每一行、每一列以及每一条对角线上的三个点图的点数之和均相等,如图给出了《河图》的部分点图,请你推算出P处所对应点图的点数是( )
我国古代的《河图》是由3×3的方格构成,每个方格均有数目不同的点图,每一行、每一列以及每一条对角线上的三个点图的点数之和均相等,如图给出了《河图》的部分点图,请你推算出P处所对应点图的点数是( )


