题目内容
 如图,已知矩形ABCD的边AB=1,M是边AD上的动点,直线l过M与对角线AC垂直,垂足为E,且
如图,已知矩形ABCD的边AB=1,M是边AD上的动点,直线l过M与对角线AC垂直,垂足为E,且| AE |
| EC |
| 1 |
| 4 |
(1)若直线l过B点,求AD的长;
(2)写出AD的取值范围,不必说明理由;
(3)若直线l分矩形ABCD的两部分的面积比是1:10,设直线l与矩形的另一边相交于H,AH=x.请用含x的代数式表示AD.
考点:相似形综合题
专题:
分析:(1)根据两角相等的两个三角形相似,可得△ABE∽△BCE,根据形似三角形的性质,可得
=
=
,根据等量代换,可得答案;
(2)根据△ABE∽△BCE,可得
=
或
=
,可得答案;
(3)根据三角形相似,可得
=
,根据面积的比,可得即
=
,根据等量代换,可得AM2,根据等比形式,可得答案.
| AB |
| BC |
| AE |
| BE |
| BE |
| CE |
(2)根据△ABE∽△BCE,可得
| AB |
| BC |
| 1 |
| 2 |
| AB |
| BC |
| 2 |
| 1 |
(3)根据三角形相似,可得
| AH |
| AM |
| AD |
| DC |
| ||
| AD |
| 1 |
| 11 |
解答:解:(1)∵∠ABE=∠BCE,∠AEB=∠BEC,
∴△ABE∽△BCE,
∴
=
=
∵
=
,
∴
=
∵AB=1,
∴AD=BC=2;
(2)
≤x≤2;
(3)当直线l过点B时,可分矩形梁部分的面积是
,则H必在AB上,
∵△AHM∽△DCA,
∴
=
∵CD=1,
∴
=AD
依题意可知,
=
∴
=
,即
=
,
∴AM 2=
,
AM=
即AD=
x.
∴△ABE∽△BCE,
∴
| AB |
| BC |
| AE |
| BE |
| BE |
| CE |
∵
| AE |
| EC |
| 1 |
| 4 |
∴
| AB |
| BC |
| 1 |
| 2 |
∵AB=1,
∴AD=BC=2;
(2)
| 1 |
| 2 |
(3)当直线l过点B时,可分矩形梁部分的面积是
| 1 |
| 7 |
∵△AHM∽△DCA,
∴
| AH |
| AM |
| AD |
| DC |
∵CD=1,
∴
| AH |
| AM |
依题意可知,
| S△AMH |
| S矩形ABCD |
| 1 |
| 11 |
∴
| ||
| AD•DC |
| 1 |
| 11 |
| ||
| AD |
| 1 |
| 11 |
∴AM 2=
| 2 |
| 11 |
AM=
| ||
| 11 |
即AD=
| ||
| 2 |
点评:本题考查了相似综合题,利用了相似三角形的判定与性质,利用了面积的比,得出AM的值是解题关键.

练习册系列答案
相关题目

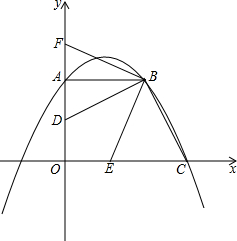 如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在第一象限,点C的坐标为(3,0).AB∥x轴,且OA=AB,抛物线y=ax2+bx+2经过点A、B、C.连 结BC,过点B作BD⊥BC,交OA于点D.将∠CBD绕点B按顺时针方向旋转得到∠EBF,角的两边分别交x轴的正半轴、y轴的正半轴于E、F.
如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在第一象限,点C的坐标为(3,0).AB∥x轴,且OA=AB,抛物线y=ax2+bx+2经过点A、B、C.连 结BC,过点B作BD⊥BC,交OA于点D.将∠CBD绕点B按顺时针方向旋转得到∠EBF,角的两边分别交x轴的正半轴、y轴的正半轴于E、F. 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BC于点E.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BC于点E. 某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为
某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为 某校根据去年初三学生参加中考的数学成绩的等级,绘制成如图的扇形统计图,则图中表示A等级的扇形的圆心角的大小为
某校根据去年初三学生参加中考的数学成绩的等级,绘制成如图的扇形统计图,则图中表示A等级的扇形的圆心角的大小为