题目内容
△ABC，点D在AB上，AD=AC，连接CD，点E，F分别在线段BC、射线CA上，∠EDF=∠ACB，点G在DF上，DG•BC=A•DE
（1）如图，求证：∠DGE=∠BAC；
（2）若AD=3BD，cos∠BAC=
，射线CG交AB于点H，探究线段DH，FA，FC之间的数量关系，并证明你的结论．
（1）如图，求证：∠DGE=∠BAC；
（2）若AD=3BD，cos∠BAC=
| 7 |
| 8 |
考点：相似形综合题
专题：
分析：（1）根据等式的性质，可得
=
，根据相似三角形的判定与性质，可得答案；
（2）根据勾股定理，可得BP=
k，根据两边对应成比例及夹角相等的两个三角形相似，可得△CBD∽△ABC，根据相似三角形的性质，可得
=
，根据两边对应成比例及夹角相等的两个三角形相似，可得△CGO∽△EDO，根据∠GCD=∠ABC，∠CHD=∠BHC，可得△CHD∽△BHC，根据相似三角形的性质，可得
=
=
=
，根据等式的性质，可得答案．
| DG |
| AC |
| DE |
| CB |
（2）根据勾股定理，可得BP=
| 15 |
| CD |
| AC |
| BC |
| AB |
| CH |
| BH |
| HD |
| HC |
| CD |
| BC |
| 3 |
| 4 |
解答：（1）证明：∵DG•BC=AD•DE，
∴
=
．
∵AD=AC，
∴
=
．
∵∠EDG=∠ACB，
∴△EDG∽△BCA．
∴∠DGE=∠BAC；
（2）如图2当点F在AC上时，作BP⊥AC与P点，设AB=8k，由cos∠BAC=
=
得AP=7k，
∵AD=3DB，
∴AC=AD=6k，PC=k．
在Rt△ABP内，AB=8k，AP=7k，
∴BP=
k，
在Rt△BCP内PC=k，BP=
k，
∴BC=4k
∵BD=2k，
∴
=
，
∵∠CBD=∠ABC，
∴△CBD∽△ABC，
∴∠DCB=∠BAC，
=
∴CD=
BC
设EG交CD于点O，
由∠DCB=∠A=∠DGE，∠GOD=EOC，
∴△GOD∽△COE，
∴
=
，
=
∵∠COG=∠EOD，
∴△CGO∽△EDO，
∴∠GCD=∠GED．
由（1）△EDG∽△BCA得∠GED=∠ABC，
∴∠GCD=∠ABC，
∵∠CHD=∠BHC，
∴△CHD∽△BHC，
∴
=
=
=
，
设HD=3t，CH=4t，BH=
t
∴BD=
t=2k
∴HD=
k
∵FA+FC=6k，
∴FA+FC=
HD，
如图3当点F在CA延长线上时，FC-FA=
HD．
∴
| DG |
| AD |
| DE |
| BC |
∵AD=AC，
∴
| DG |
| AC |
| DE |
| CB |
∵∠EDG=∠ACB，
∴△EDG∽△BCA．
∴∠DGE=∠BAC；
（2）如图2当点F在AC上时，作BP⊥AC与P点，设AB=8k，由cos∠BAC=
| AP |
| AB |
| 7 |
| 8 |
∵AD=3DB，
∴AC=AD=6k，PC=k．
在Rt△ABP内，AB=8k，AP=7k，
∴BP=
| 15 |
在Rt△BCP内PC=k，BP=
| 15 |
∴BC=4k
∵BD=2k，
∴
| BD |
| BC |
| BC |
| AB |
∵∠CBD=∠ABC，
∴△CBD∽△ABC，
∴∠DCB=∠BAC，
| CD |
| AC |
| BC |
| AB |
∴CD=
| 3 |
| 4 |
设EG交CD于点O，
由∠DCB=∠A=∠DGE，∠GOD=EOC，
∴△GOD∽△COE，
∴
| OG |
| CO |
| OD |
| OE |
| OG |
| OD |
| OC |
| OE |
∵∠COG=∠EOD，
∴△CGO∽△EDO，
∴∠GCD=∠GED．
由（1）△EDG∽△BCA得∠GED=∠ABC，
∴∠GCD=∠ABC，
∵∠CHD=∠BHC，
∴△CHD∽△BHC，
∴
| CH |
| BH |
| HD |
| HC |
| CD |
| BC |
| 3 |
| 4 |
设HD=3t，CH=4t，BH=
| 16 |
| 3 |
∴BD=
| 7 |
| 3 |
∴HD=
| 18 |
| 7 |
∵FA+FC=6k，
∴FA+FC=
| 7 |
| 3 |
如图3当点F在CA延长线上时，FC-FA=
| 7 |
| 3 |
点评：本题考查了相似形综合题，利用了相似三角形的判定与性质，多次利用相似三角形的判定与性质是解题关键．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
如图，在?ABCD中，BC=10，sinB=
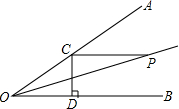如图，∠AOB=30°，P是∠AOB的平分线上一点，PC∥OB，交OA于C，CD⊥OB于D．若PC=3，则CD的长为
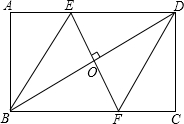如图，在矩形ABCD中，边AB的长为3，点E，F分别在AD，BC上，连接BE，DF，EF，BD．若四边形BEDF是菱形，且EF=AE+FC，则边BC的长为（ ）
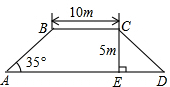如图，某堤坝横断面为梯形ABCD，若斜坡AB的坡角∠BAD为35゜，斜坡CD的坡度为i=1：1.2（垂直高度CE与水平宽度DE的比），上底BC=10m，堤坝高度CE=5m，求下底AD的长度？（结果精确到0.1m，参考数据：sin35゜≈0.57，cos 35゜≈0.82，tan35゜≈0.70）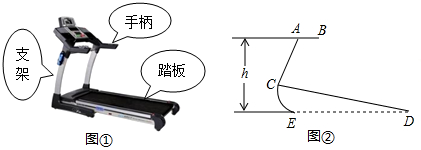
如图，已知矩形ABCD的边AB=1，M是边AD上的动点，直线l过M与对角线AC垂直，垂足为E，且