题目内容
一个平行四边形两对角之和为116°,则相邻的两内角分别是__________和_________.
 58° 122°
【解析】试题解析:
如图所示:
∵四边形ABCD是平行四边形,
故答案为:58°;122°.
58° 122°
【解析】试题解析:
如图所示:
∵四边形ABCD是平行四边形,
故答案为:58°;122°.
 阅读快车系列答案
阅读快车系列答案与 形状相同的抛物线解析式为( )
形状相同的抛物线解析式为( )
A. y=
B. 
C. 
D. 
 D
【解析】抛物线的形状只与a有关,a相等,形状就相同,∴中,a=2.
故选:D.
D
【解析】抛物线的形状只与a有关,a相等,形状就相同,∴中,a=2.
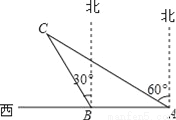
故选:D. 如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: 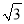 ≈1.732)
≈1.732)
 17.
【解析】试题分析:过点C作CD⊥AB于点D,则若该船继续向西航行至离灯塔距离最近的位置为CD的长度,利用锐角三角函数关系进行求解即可.
试题解析:如图,过点C作CD⊥AB于点D,
AB=20×1=20(海里),∵∠CAF=60°,∠CBE=30°,∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,∴∠C=180°﹣∠CBA﹣∠CAB=30°,∴...
17.
【解析】试题分析:过点C作CD⊥AB于点D,则若该船继续向西航行至离灯塔距离最近的位置为CD的长度,利用锐角三角函数关系进行求解即可.
试题解析:如图,过点C作CD⊥AB于点D,
AB=20×1=20(海里),∵∠CAF=60°,∠CBE=30°,∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,∴∠C=180°﹣∠CBA﹣∠CAB=30°,∴... 如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )

A. 100 B. 200 C. 100 D. 200
B. 200 C. 100 D. 200
 B
【解析】试题分析:根据方位角可得:∠A=30°,∠CBA=120°,则∠C=30°,则△ABC为等腰三角形,故BC=AB=200m,故选B.
B
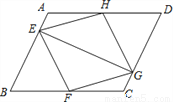
【解析】试题分析:根据方位角可得:∠A=30°,∠CBA=120°,则∠C=30°,则△ABC为等腰三角形,故BC=AB=200m,故选B. ( 本小题满分10分)如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:
⑴△AEH≌△CGF;
⑵四边形EFGH是菱形.
 (1)证明见试题解析;(2)证明见试题解析.
【解析】试题分析:(1)、由全等三角形的判定定理SAS证得结论;(2)、易证四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH是菱形.
试题解析:(1)、如图,∵四边形ABCD是平行四边形, ∴∠A=∠C,
...
(1)证明见试题解析;(2)证明见试题解析.
【解析】试题分析:(1)、由全等三角形的判定定理SAS证得结论;(2)、易证四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH是菱形.
试题解析:(1)、如图,∵四边形ABCD是平行四边形, ∴∠A=∠C,
... 平行四边形的一条边长是12cm,那么它的两条对角线的长可能是( )
A. 8cm和16cm B. 10cm和16cm C. 8cm和14cm D. 8cm和12cm
 B
【解析】试题解析:对于A,两条对角线的一半长分别为4cm,8cm,由于4+8=12,故不能构成三角形,故A不符合题意;
对于B,两条对角线的一半长分别为5cm,8cm,由于5+8>12,故能构成三角形,故B符合题意;
对于C,两条对角线的一半长分别为4cm,7cm,由于4+7<12,故不能构成三角形,故C不符合题意;
对于D,两条对角线的一半长分别为4cm,6cm,由于...
B
【解析】试题解析:对于A,两条对角线的一半长分别为4cm,8cm,由于4+8=12,故不能构成三角形,故A不符合题意;
对于B,两条对角线的一半长分别为5cm,8cm,由于5+8>12,故能构成三角形,故B符合题意;
对于C,两条对角线的一半长分别为4cm,7cm,由于4+7<12,故不能构成三角形,故C不符合题意;
对于D,两条对角线的一半长分别为4cm,6cm,由于... 如图,在?ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
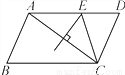
A. 7 B. 10 C. 11 D. 12
 B
【解析】试题分析:根据线段垂直平分线的性质可得AE=EC,再根据平行四边形的性质可得DC=AB=4,AD=BC=6,进而可以算出△CDE的周长.
【解析】
∵AC的垂直平分线交AD于E,
∴AE=EC,
∵四边形ABCD是平行四边形,
∴DC=AB=4,AD=BC=6,
∴△CDE的周长为:EC+CD+ED=AD+CD=6+4=10,
故选:B.
...
B
【解析】试题分析:根据线段垂直平分线的性质可得AE=EC,再根据平行四边形的性质可得DC=AB=4,AD=BC=6,进而可以算出△CDE的周长.
【解析】
∵AC的垂直平分线交AD于E,
∴AE=EC,
∵四边形ABCD是平行四边形,
∴DC=AB=4,AD=BC=6,
∴△CDE的周长为:EC+CD+ED=AD+CD=6+4=10,
故选:B.
... 四边形ABCD中,若∠A+∠C+∠D=280°,则∠B的度数为( )
A. 80° B. 90° C. 170° D. 20°
 A
【解析】试题分析:四边形的内角和为360°,
∴∠B=360°-(∠A+∠C+∠D)
=360°-280°
=80°,
故选A.
A
【解析】试题分析:四边形的内角和为360°,
∴∠B=360°-(∠A+∠C+∠D)
=360°-280°
=80°,
故选A. 

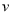 ,该船在流水(速度为
,该船在流水(速度为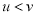 )中从上游A驶往下游B,再返回A,所用的时间为T,假设
)中从上游A驶往下游B,再返回A,所用的时间为T,假设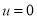 ,即河流改为静水,该船从A至B再返回A,所用时间为
,即河流改为静水,该船从A至B再返回A,所用时间为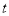 ,则( )
,则( )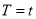 B.
B. 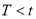 C.
C. 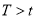 D. 不能确定T与
D. 不能确定T与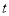 的大小关系
的大小关系