题目内容

在梯形ABCD中，AD∥BC，那么∠A：∠B：∠C：∠D可能为（　　）
A、3：4：5：2
B、2：3：4：5
C、5：3：4：2
D、5：4：3：2
考点：梯形
专题：
分析：根据两直线平行同旁内角互补，可得∠A+∠B=∠C+∠D，从而可确定答案．
解答：解：A、3+4=5+2，则选项正确；
B、2+3≠4+5，则选项错误；
C、5+3≠4+2，选项错误；
D、5+4≠3+2，选项错误．
故选A．
点评：本题考查梯形的性质，根据两直线平行同旁内角互补，即可得到同一底上的两个底角互补．
练习册系列答案
相关题目
当x≠
 
时，分式
3
1-x
有意义．当x
 
时，分式
x-2
3x+8
无意义．
已知x-3y=2，x+y=5，则x2-2xy-3y2=
 
．
已知关于x的方程x2+kx-2=0的一个根是1，则它的另一个根是（　　）
A、-3B、3C、-2D、2
已知一个多项式（m+1）x3y|m|+xy2+85是个四次三项式，那么m=（　　）
A、1B、-1C、±1D、0
有理数m，n在数轴上的位置如图．则下列关系中正确的个数是（　　）
（1）m+n＜0；（2）n-m＞0；（3）2m-n＞0；（4）-m-n＞0；（5）
1
m
＞-
1
n
．
A、1个B、2个C、3个D、4个
颜色和形状大小一样盒子，第一个盒子里装有10个黑球，第二个盒子里装有7个红球，第三个盒子里装有9个黄球，全部26个球除颜色形状大小完全一样；若随机打开一个盒子后摸到是黑球的概率是（　　）
A、
5
13
B、
1
2
C、
1
3
D、1
已知如图，一次函数y=kx+b的图象与反比例函数y=
n
x
的图象交于A（-3，1），B（1，m）两点．
（1）求上述反比例函数和一次函数的表达式；
（2）求△AOB的面积．
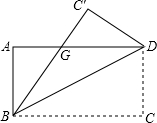如图，一张矩形纸片ABCD，其中AD=8cm，AB=6cm，先沿对角线BD对折，点C落在点C′的位置，BC′交AD于点G．
（1）求证：AG=C′G；
（2）求△BDG的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网