Question

19．如图，梯形ACDB的两条角平分线交BD于点G，若AB=2，AC=6，BD=5，CD=4．

Answer 1

分析 延长CG交AB延长线与点E，根据AG平分∠CAB，CG平分∠ACD，得∠CAG+∠ACG=$\frac{1}{2}$∠CAB+$\frac{1}{2}$∠ACD=$\frac{1}{2}$（∠CAB+∠ACD），又四边形ACBD是梯形知∠ACD+∠CAB=180°，故∠CAG+∠ACG=$\frac{1}{2}$（∠CAB+∠ACD）=90°即AG⊥CE，结合AG平分∠CAB根据三线合一得△CAE为等腰三角形，进而得出AC=AE=6、CG=EG，因为∠BEG=∠DCG、∠BEG=∠DCG可判定△CDG≌△EBG，得出CD=EB=AE-AB=4．

解答 解：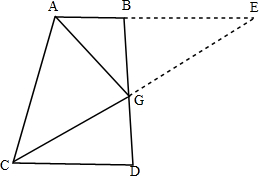

如图，延长CG交AB延长线与点E，
∵四边形ACBD是梯形，
∴∠ACD+∠CAB=180°，∠BEG=∠DCG，
∵AG平分∠CAB，CG平分∠ACD，
∴∠CAG=$\frac{1}{2}$∠CAB，∠ACG=$\frac{1}{2}$∠ACD，
则∠CAG+∠ACG=$\frac{1}{2}$∠CAB+$\frac{1}{2}$∠ACD=$\frac{1}{2}$（∠CAB+∠ACD）=90°，
∴∠AGD=90°，即AG⊥CE，
∵AG平分∠CAB，
∴△CAE为等腰三角形，即CG=EG，AC=AE=6，
∵AB=2，
∴BE=4，
在△CDG和△EBG中，
∵$\left\{\begin{array}{l}{∠DCG=∠BEG}\\{CG=EG}\\{∠CGD=∠EGB}\end{array}\right.$，
∴△CDG≌△EBG（ASA），
∴CD=EB=4，
故答案为：4．

点评 本题主要考查等腰三角形和全等三角形的判定和性质等知识点，添加辅助线构建全等三角形是解题关键．