题目内容
已知a,3是直角三角形的两边,第三边的长满足方程x2-9x+20=0,则a的值为 .
考点:勾股定理,解一元二次方程-因式分解法
专题:分类讨论
分析:求出方程的解,得出直角三角形的两边长,分为两种情况:①当a和3是两直角边时,②当a是斜边时,根据勾股定理求出第三边即可.
解答:解:∵x2-9x+20=0,即(x-4)(x-5)=0,
∴x-4=0,x-5=0,解得,x1=5,x2=4,
当a和3是两直角边时,第三边是5或4,
∴a=4或
当a是斜边时,第三边
,
故答案为:4或
或
.
∴x-4=0,x-5=0,解得,x1=5,x2=4,
当a和3是两直角边时,第三边是5或4,
∴a=4或
| 7 |
当a是斜边时,第三边
| 41 |
故答案为:4或
| 7 |
| 41 |
点评:本题考查了利用勾股定理解直角三角形的能力,当已知条件中没有明确哪是斜边时,要注意讨论,一些学生往往忽略这一点,造成丢解.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
用一个平面去截圆锥,截面图形不可能是( )
A、 |
B、 |
C、 |
D、 |
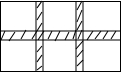 如图是宽为30m,长为44m的矩形草皮,要修筑同样宽的三条水渠(两条纵向,一条横向,且互相垂直),把草皮分成六块,要使余下草皮的面积为1120m2,求水渠宽为多少米?
如图是宽为30m,长为44m的矩形草皮,要修筑同样宽的三条水渠(两条纵向,一条横向,且互相垂直),把草皮分成六块,要使余下草皮的面积为1120m2,求水渠宽为多少米?
 如图,过A点画与直线BC垂直的线段,A点到BC的距离是线段
如图,过A点画与直线BC垂直的线段,A点到BC的距离是线段