Question

5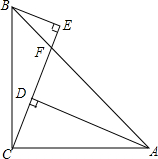．如图，AD=CE=24，BC=25，∠BCE=∠CAD，BE∥AD，BF：AF=7：24，给出下列结论：①∠E=90°；②∠BCA=90°；③∠BAC=45°；④AB=25$\sqrt{3}$．其中正确的结论有①②③．（把所有正确结论序号都填在横线上）

Answer 1

分析 （1）由BE∥AD，得出$\frac{BE}{AD}$=$\frac{BF}{AF}$，解得：BE=7，得出BE²+CE²=BC²，即可证得∠E=90°；
（2）由BE∥AD，得出∠ADC=90°，∠DCA+∠CAD=90°，再由∠BCE=∠CAD，即可证得∠BCA=90°；
（3）由ASA证得△BCE≌△CAD，得出BC=AC，即可证得∠BAC=45°；
（4）由△ABC为等腰直角三角形，求得AB=25$\sqrt{2}$，即可得出结论．

解答 解：（1）∵BE∥AD，
∴$\frac{BE}{AD}$=$\frac{BF}{AF}$，
即$\frac{BE}{24}$=$\frac{7}{24}$，
解得：BE=7，
∵7²+24²=25²，
即BE²+CE²=BC²，
∴△BEC是直角三角形，
∴∠E=90°，
∴①正确；
（2）∵BE∥AD，∠E=90°，
∴∠ADC=90°，∠DCA+∠CAD=90°，
∵∠BCE=∠CAD，
∴∠DCA+∠BCE=90°，
即∠BCA=90°，
∴②正确；
（3）在△BCE和△CAD中，
$\left\{\begin{array}{l}{∠BCE=∠DAC}\\{AD=CE}\\{∠E=∠ADC=90°}\end{array}\right.$，
∴△BCE≌△CAD（ASA），
∴BC=AC，
∵∠BCA=90°
∴∠BAC=45°，
∴③正确；
（4）∵BC=AC，∠BCA=90°，
∴AB=$\sqrt{2}$BC=25$\sqrt{2}$，
∴④错误．
故答案为：①②③．

点评 本题考查了全等三角形的判定与性质、平行线分线段成比例定理、勾股定理的逆定理、等腰直角三角形的性质等知识；本题综合性强，有一定难度．