题目内容
平行四边形两邻边分别为24和16，若两长边间的距离为8，则两短边间的距离为（ ）
| A、5 | B、6 | C、8 | D、12 |
考点：平行四边形的性质
专题：
分析：首先设两短边间的距离为x，由平行四边形两邻边分别为24和16，若两长边间的距离为8，可得24×8=16x，继而求得答案．
解答：解：设两短边间的距离为x，
∵平行四边形两邻边分别为24和16，若两长边间的距离为8，
∴24×8=16x，
解得：x=12．
∴两短边间的距离为12．
故选D．
∵平行四边形两邻边分别为24和16，若两长边间的距离为8，
∴24×8=16x，
解得：x=12．
∴两短边间的距离为12．
故选D．
点评：此题考查了平行四边形的性质．此题难度不大，注意掌握方程思想的应用．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
如图，AB∥CD，CP交AB与O，∠A=∠P，若∠C=50°，则∠A=
如图，已知△ABC中，DE∥BC，将△ADE沿DE翻折，使得点A落在平面内的A′处，若∠B=50°，则∠BDA′的度数是（ ）
| A、90° | B、100° |
| C、80° | D、70° |
最薄的金箔的厚度为0.000000091m，用科学记数法表示0.000000091这个数正确的是（ ）
| A、9.1×10-7 |
| B、9.1×10-8 |
| C、0.91×10-7 |
| D、0.91×10-8 |
下列语句中，不是命题的是（ ）
| A、同位角相等，两直线平行 |
| B、若a2=b2，则a=b |
| C、画直线AB平行于CD |
| D、同角的余角相等 |
下列关系式中，正确的是（ ）
| A、（a-b）2=a2-b2 |
| B、（a+b）（a-b）=a2+b2 |
| C、（a+b）2=a2+b2 |
| D、（a+b）2=a2+2ab+b2 |
某项工作，甲单独做要4天完成，乙单独做要6天完成，若甲先做1天后，然后甲、乙合作完成此项工作，若设甲一共做了x天，所列方程是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知点M（2，3）在双曲线y=
上，则下列各点一定不在该双曲线上的是（ ）
| k |
| x |
| A、（3，2） |
| B、（-2，-3） |
| C、（1，6） |
| D、（3，-2） |
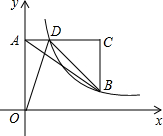如图，在平面直角坐标系中，点A在y轴正半轴上，AC∥x轴，点B、C的横坐标都是3，且BC=2，点D在AC上，若反比例函数y=