题目内容
16.不等式组$\left\{\begin{array}{l}{x≥2}\\{x>3}\end{array}\right.$的解集在数轴上表示为( )| A. | 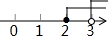 | B. | 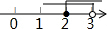 | ||
| C. | 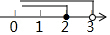 | D. | 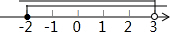 |
分析 利用不等式组取解集的方法确定出解集,表示在数轴上即可.
解答 解:不等式组$\left\{\begin{array}{l}{x≥2}\\{x>3}\end{array}\right.$,
解得:x>3,
表示在数轴上,如图所示: ,
,
故选A
点评 此题考查了在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
4.已知a+b=2,a-b=-3,则a2-b2的值为( )
| A. | 6 | B. | -6 | C. | -$\frac{3}{2}$ | D. | -5 |
11.阅读下面材料,并解答其后的问题:
定义:两组领边分别相等的四边形叫做筝形.
如图1,四边形ABCD中,若AD=AB,CD=CB,则四边形ABCD是筝形.
类比研究:
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对平行四边形的性质进行研究,请根据示例图形,完成下表:
(1)表格中①、②分别填写的内容是:
①轴对称图形;
②一条对角线垂直平分另一条对角线.
(2)演绎论证:证明筝形有关对角线的性质.
已知:在筝形ABCD中,AD=AB,BC=DC,AC、BD是对角线.
求证:AC垂直平分BD.
证明:
(3)运用:如图3,已知筝形ABCD中,AD=AB=4,CD=CB,∠A=90°,∠C=60°,求筝形ABCD的面积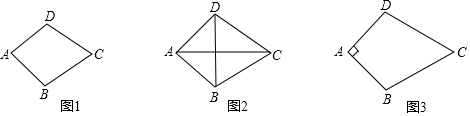
定义:两组领边分别相等的四边形叫做筝形.
如图1,四边形ABCD中,若AD=AB,CD=CB,则四边形ABCD是筝形.
类比研究:
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对平行四边形的性质进行研究,请根据示例图形,完成下表:
| 四边形 | 示例图形 | 对称性 | 边 | 角 | 对角线 |
| 平行 四边形 |  | 两组对边分别平行,两组对边分别相等 | 两组对边分别平行,两组对边分别相等. | 两组对角 分别相等. | 对角线互相平分. |
| 等腰 梯形 | 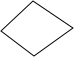 | ①轴对称图形 | 两组邻边分别相等 | 有一组对角相等 | ②一条对角线垂直平分另一条对角线 |
①轴对称图形;
②一条对角线垂直平分另一条对角线.
(2)演绎论证:证明筝形有关对角线的性质.
已知:在筝形ABCD中,AD=AB,BC=DC,AC、BD是对角线.
求证:AC垂直平分BD.
证明:
(3)运用:如图3,已知筝形ABCD中,AD=AB=4,CD=CB,∠A=90°,∠C=60°,求筝形ABCD的面积

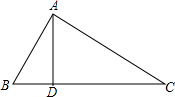 如图,在△ABC中,D是边BC上一点,若AB=10,BD=6,AD=8,AC=17,求BC的长.
如图,在△ABC中,D是边BC上一点,若AB=10,BD=6,AD=8,AC=17,求BC的长.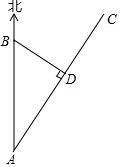 如图所示,沿海城市B的正南方向A处有一台风中心,沿AC的方向以30km/h的速度移动,已知AC所在的方向与正北成30°的夹角,B市距台风中心最短的距离BD为120km,求台风中心从A处到达D处需要多少小时?($\sqrt{3}≈1.73$,结果精确到0.1)
如图所示,沿海城市B的正南方向A处有一台风中心,沿AC的方向以30km/h的速度移动,已知AC所在的方向与正北成30°的夹角,B市距台风中心最短的距离BD为120km,求台风中心从A处到达D处需要多少小时?($\sqrt{3}≈1.73$,结果精确到0.1) 如图,在边长为4的正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD.
如图,在边长为4的正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD.