题目内容
18. 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4,设AB=x,AD=y,则x2+(y-4)2的值为( )
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4,设AB=x,AD=y,则x2+(y-4)2的值为( )| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
分析 根据矩形的性质得到CD=AB=x,BC=AD=y,然后利用直角△BDE的斜边上的中线等于斜边的一半得到:BF=DF=EF=4,则在直角△DCF中,利用勾股定理求得x2+(y-4)2=DF2.
解答 解:∵四边形ABCD是矩形,AB=x,AD=y,
∴CD=AB=x,BC=AD=y,∠BCD=90°.
又∵BD⊥DE,点F是BE的中点,DF=4,
∴BF=DF=EF=4.
∴CF=4-BC=4-y.
∴在直角△DCF中,DC2+CF2=DF2,即x2+(4-y)2=42=16,
∴x2+(y-4)2=x2+(4-y)2=16.
故选:D.
点评 本题考查了勾股定理,直角三角形斜边上的中线以及矩形的性质.根据“直角△BDE的斜边上的中线等于斜边的一半”求得BF的长度是解题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 在四边形ABCD中,AC=BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
在四边形ABCD中,AC=BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
 在四边形ABCD中,AC=BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
在四边形ABCD中,AC=BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )| A. | 64 | B. | 18 | C. | 36 | D. | 48 |
3.有甲、乙、丙三个村庄分别位于等边△ABC的顶点,在城中村改造时,为保护环境,改善居民的生活条件,政府决定铺设能够连结这三个村庄的天然气管道.设计人员给出了如图四个设计方案(点D为BC边的中点,点O为△ABC的中心,实线表示天然气管道),其中天然气管道总长最短的是( )
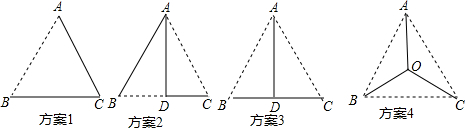

| A. | 方案1 | B. | 方案2 | C. | 方案3 | D. | 方案4 |
10.(-3)×3的结果是( )
| A. | -9 | B. | 9 | C. | 0 | D. | -6 |
 《孙子算经》是中国古代重要的数学著作,约成书于一千五百年前,共三卷,卷上叙述算筹记数的纵横相间制度和筹算乘除法,记有许多有趣的问题.其中记载:“今有木,不知长短,引绳度之,余绳四尺无寸;屈绳量之,不足一尺.木长几何?”
《孙子算经》是中国古代重要的数学著作,约成书于一千五百年前,共三卷,卷上叙述算筹记数的纵横相间制度和筹算乘除法,记有许多有趣的问题.其中记载:“今有木,不知长短,引绳度之,余绳四尺无寸;屈绳量之,不足一尺.木长几何?” 如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC中点,若S△ABC=12,则S△ADF-S△BEF=2.
如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC中点,若S△ABC=12,则S△ADF-S△BEF=2.