题目内容
13.如果△ABC∽△DEF,且对应高之比为2:3,那么△ABC和△DEF的面积之比是4:9.分析 根据相似三角形的性质求出两个三角形的相似比,根据相似三角形面积的比等于相似比的平方得到答案.
解答 解:∵△ABC∽△DEF,对应高之比为2:3,
∴△ABC和△DEF的相似比为2:3,
∴△ABC和△DEF的面积之比是4:9,
故答案为:4:9.
点评 本题考查的是相似三角形的性质,相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 如图,抛物线y=x2-2x-3与x轴交于点A、D,与y轴交于点C,四边形ABCD是平行四边形,则点B的坐标是( )
如图,抛物线y=x2-2x-3与x轴交于点A、D,与y轴交于点C,四边形ABCD是平行四边形,则点B的坐标是( )
 如图,抛物线y=x2-2x-3与x轴交于点A、D,与y轴交于点C,四边形ABCD是平行四边形,则点B的坐标是( )
如图,抛物线y=x2-2x-3与x轴交于点A、D,与y轴交于点C,四边形ABCD是平行四边形,则点B的坐标是( )| A. | (-4,-3) | B. | (-3,-3) | C. | (-3,-4) | D. | (-4,-4) |
2. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )| A. | (-4,3) | B. | (3,4) | C. | (-3,4) | D. | (4,3) |
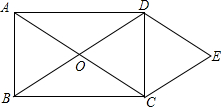 如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.