题目内容
16.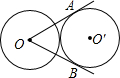 两个等圆⊙O和⊙O′外切,过⊙O作⊙O′的两条切线OA、OB、A、B是切点,则∠AOB等于多少度?
两个等圆⊙O和⊙O′外切,过⊙O作⊙O′的两条切线OA、OB、A、B是切点,则∠AOB等于多少度?
分析 利用两圆的半径分别为R和r,外切时P=R+r,进而得出OO′=2O′A,即可得出∠AOO′=30°,再求出答案即可.
解答  解:连接O′A,OO′,
解:连接O′A,OO′,
∵过⊙O作⊙O′的两条切线OA、OB、A、B是切点,
∴O′A⊥OA,∠AOO′=∠BOO′,
又∵OO′=2O′A,
∴∠AOO′=30°,
∴∠AOB=2∠AOO′=60°.
点评 本题考查了切线的性质以及相切两圆的性质,得出OO′=2O′A是解题关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
8.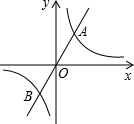 如图,正比例函数y1=k1x和反比例函数y2=$\frac{k2}{x}$的图象交于A(1,2),B两点,给出下列结论:①k1<k2;②当x<-1时,y1<y2;③当y1>y2时,y2随x的增大而减小;④当x<0时,y2随x的增大而减小.其中正确的有( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{k2}{x}$的图象交于A(1,2),B两点,给出下列结论:①k1<k2;②当x<-1时,y1<y2;③当y1>y2时,y2随x的增大而减小;④当x<0时,y2随x的增大而减小.其中正确的有( )
 如图,正比例函数y1=k1x和反比例函数y2=$\frac{k2}{x}$的图象交于A(1,2),B两点,给出下列结论:①k1<k2;②当x<-1时,y1<y2;③当y1>y2时,y2随x的增大而减小;④当x<0时,y2随x的增大而减小.其中正确的有( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{k2}{x}$的图象交于A(1,2),B两点,给出下列结论:①k1<k2;②当x<-1时,y1<y2;③当y1>y2时,y2随x的增大而减小;④当x<0时,y2随x的增大而减小.其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
5.小明的爸爸买回两块地毯,他告诉小明小地毯的面积正好是大地毯面积的$\frac{1}{3}$,且两块地毯的面积和为20平方米,小明很快便得出了两块地毯的面积为(单位:平方米)( )
| A. | $\frac{40}{3}$,$\frac{20}{3}$ | B. | 30,10 | C. | 15,5 | D. | 12,8 |
6.A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/小时,乙车速度为80千米/小时,经过t小时两车相距50千米.则t的值是( )
| A. | 2 | B. | 2或2.25 | C. | 2.5 | D. | 2或2.5 |
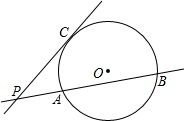 已知:CP为圆O切线,AB为圆的割线,CP、AB交于P,求证:AP•BP=CP2.
已知:CP为圆O切线,AB为圆的割线,CP、AB交于P,求证:AP•BP=CP2.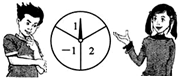 如图,一转盘被等分成三个扇形,上面分别标有-1,2,指针位置固定,转动转盘后任其自由停止后,某个扇形会恰好停在指针所指的位置,得到这个扇形上相应的数.若指针恰好指在等分线上,则需重新转动转盘.
如图,一转盘被等分成三个扇形,上面分别标有-1,2,指针位置固定,转动转盘后任其自由停止后,某个扇形会恰好停在指针所指的位置,得到这个扇形上相应的数.若指针恰好指在等分线上,则需重新转动转盘.