题目内容
1.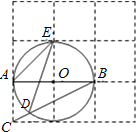 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的余弦值等于( )
如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的余弦值等于( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
分析 由圆周角定理可知∠AED=∠ABC,在Rt△BAC中,由AB=2,AC=1通过勾股定理以及余弦定义,即可得出结论.
解答 解:在Rt△BAC中,由勾股定理可得:
BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{5}$,
cos∠ABC=$\frac{AB}{BC}$=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
∵∠AED=∠ABC(同弦圆周角相等),
∴cos∠AED=$\frac{2\sqrt{5}}{5}$.
故选A.
点评 本题考查了圆周角定理、勾股定理以及三角函数中余弦的定义,解题的关键是找到与∠AED相等的角.本题属于基础题,没有难度,解决此类型题目时,需细心观察图形,在直角三角形中找到与所求角相等的角.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
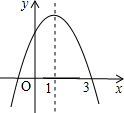 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,下列结论: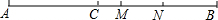 如图,点C是线段AB上一点,M、N分别是AB、CB的中点,AC=8cm,NB=5cm,求线段MN的长.
如图,点C是线段AB上一点,M、N分别是AB、CB的中点,AC=8cm,NB=5cm,求线段MN的长. 如图,正方形ABCD的边长为1,P为BC上任意一点(含B、C两点),分别过点B、C、D作射线AP的垂线,垂足分别为E、F、G,以下判断:
如图,正方形ABCD的边长为1,P为BC上任意一点(含B、C两点),分别过点B、C、D作射线AP的垂线,垂足分别为E、F、G,以下判断: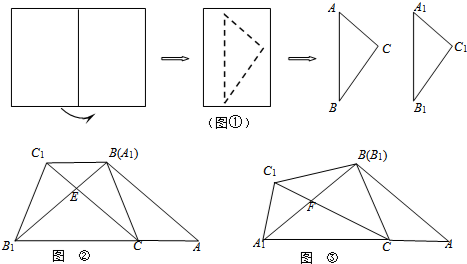
 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在边CD上,连接DE,连接BG并延长交CD于点M,交DE于点H,则HM的长为$\frac{3\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在边CD上,连接DE,连接BG并延长交CD于点M,交DE于点H,则HM的长为$\frac{3\sqrt{5}}{5}$. 如图,OP是∠MON内的一条射线,点A,B都在OP上,AC⊥OM,AD⊥ON,BE⊥OM、BF⊥ON,垂足分别为C,D,E,F,且AC=AD,求证:BE=BF.
如图,OP是∠MON内的一条射线,点A,B都在OP上,AC⊥OM,AD⊥ON,BE⊥OM、BF⊥ON,垂足分别为C,D,E,F,且AC=AD,求证:BE=BF.