题目内容
1.如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC,△A1B1C1.﹙1﹚将△ABC,△A1B1C1如图②摆放,使点A1与B重合,点B1在AC边的延长线上,连接CC1交BB1于点E.求证:∠B1C1C=∠B1BC.
﹙2﹚若将△ABC,△A1B1C1如图③摆放,使点B1与B重合,点A1在AC边的延长线上,连接CC1交A1B于点F.试判断∠A1C1C与∠A1BC是否相等,并说明理由.
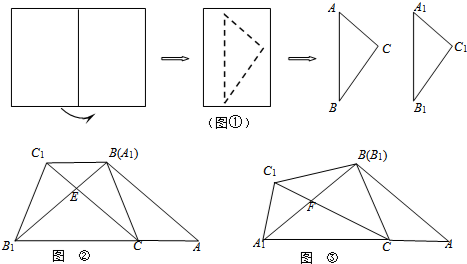
分析 (1)由题意,知△ABC≌△A1B1C1,根据矩形的性质及全等三角形的性质,可证四边形ABC1C是平行四边形,再根据平行四边形的性质及相互间的等量关系即可得出;
(2)由题意,知△ABC≌△A1B1C1,根据矩形的性质及全等三角形的性质,及相互间的等量关系即可得出.
解答 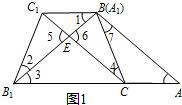 (1)证明:如图1,由题意,知△ABC≌△A1B1C1,
(1)证明:如图1,由题意,知△ABC≌△A1B1C1,
∴AB=A1B1,BC=B1C1,∠2=∠7,∠A=∠1.
∴∠3=∠A=∠1,
∴BC1∥AC.
∴四边形ABC1C是平行四边形.
∴AB∥CC1.
∴∠4=∠7=∠2.
∵∠5=∠6,
∴∠B1C1C=∠B1BC.
﹙2)解:∠A1C1C=∠A1BC.
理由如下:如图2,由题意,知△ABC≌△A1B1C1,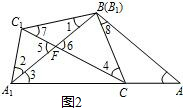
∴AB=A1B1,BC1=BC,∠1=∠8,∠A=∠2.
∴∠3=∠A,∠4=∠7.
∵∠1+∠FBC=∠8+∠FBC,
∴∠C1BC=∠A1BA.
∵∠4=$\frac{1}{2}$(180°-∠C1BC),∠A=$\frac{1}{2}$(180°-∠A1BA),
∴∠4=∠A.
∴∠4=∠2
∵∠5=∠6,
∴∠A1C1C=∠A1BC.
点评 本题考查的是翻折变换,涉及到矩形的性质及全等三角形的性质,相似三角形的判定和性质等知识点,难度较大.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
4.已知a+2b=-3,则3(2a-3b)-4(a-3b)+b的值为( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
1.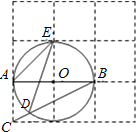 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的余弦值等于( )
如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的余弦值等于( )
 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的余弦值等于( )
如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的余弦值等于( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
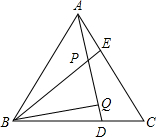 如图,△ABC为等边三角形,AE=CD,AD交BE于点P,BQ⊥AD于Q.
如图,△ABC为等边三角形,AE=CD,AD交BE于点P,BQ⊥AD于Q.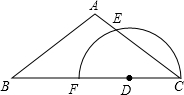 已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=$\frac{4}{5}$,AE=1.求:
已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=$\frac{4}{5}$,AE=1.求: 如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.
如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.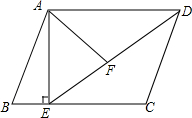 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6$\sqrt{3}$,AF=4$\sqrt{3}$,则AE的长为6.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6$\sqrt{3}$,AF=4$\sqrt{3}$,则AE的长为6.