题目内容
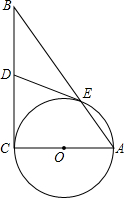 如图,AC是⊙O的直径,⊙O交AB于E,DE与⊙O的相切,D为BC的中点,
如图,AC是⊙O的直径,⊙O交AB于E,DE与⊙O的相切,D为BC的中点,(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,AE=4,求线段BC的长.
考点:切线的判定与性质
专题:
分析:(1)根据切线的判定定理只需证明AC⊥BC即可;
(2)根据勾股定理求得CE的长,然后根据相似三角形对应边成比例即可求得BC的长.
(2)根据勾股定理求得CE的长,然后根据相似三角形对应边成比例即可求得BC的长.
解答: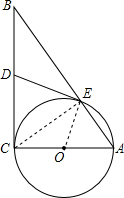 (1)证明:连接OE,CE,
(1)证明:连接OE,CE,
∵AC是直径.
∴CE⊥AB.
∵D是BC的中点,
∴DC=DB,
∴DE=BD=DC,
∴∠DCE=∠DEC.
又∵OE=OC,
∴∠OCE=∠OEC.
∴∠DCE+∠OCE=∠DEC+∠OEC.
即∠ACD=∠OED.
∵DE与⊙O的相切,
∴∠OED=90°.
∴∠ACD=90°,
∴AC⊥BC,
∴BC是⊙O的切线.
(2)解:∵⊙O的半径为6,
∴AC=12,
∴在RT△ACE中,CE=
=
=8
,
∵CE⊥AB,
∴△ACE∽△ABC,
∴
=
,
∴BC=
=
=24
.
 (1)证明:连接OE,CE,
(1)证明:连接OE,CE,∵AC是直径.
∴CE⊥AB.
∵D是BC的中点,
∴DC=DB,
∴DE=BD=DC,
∴∠DCE=∠DEC.
又∵OE=OC,
∴∠OCE=∠OEC.
∴∠DCE+∠OCE=∠DEC+∠OEC.
即∠ACD=∠OED.
∵DE与⊙O的相切,
∴∠OED=90°.
∴∠ACD=90°,
∴AC⊥BC,
∴BC是⊙O的切线.
(2)解:∵⊙O的半径为6,
∴AC=12,
∴在RT△ACE中,CE=
| AC2-CE2 |
| 122-42 |
| 2 |
∵CE⊥AB,
∴△ACE∽△ABC,
∴
| BC |
| CE |
| AC |
| AE |
∴BC=
| CE•AC |
| AE |
8
| ||
| 4 |
| 2 |
点评:此题主要考查切线的判定、圆周角定理、三角形相似的判定和性质及勾股定理等知识点的综合运用,作出辅助线根据直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知抛物线y=x2-x-1,与x轴的一个交点为(m,0),则代数式m2-m+2014的值为( )
| A、2013 | B、2015 |
| C、2014 | D、2010 |
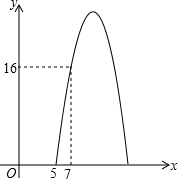 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示. 在△ABC中,AD是BC边上的高,BC=12,AD=8.矩形EFGH的顶点E、F分别在AB、AC上,H、G在BC上.
在△ABC中,AD是BC边上的高,BC=12,AD=8.矩形EFGH的顶点E、F分别在AB、AC上,H、G在BC上.
 如图所示,直线AB,CD交于点O,OE平分∠DOB,且∠AOD:∠DOE=3:1,求∠AOC的度数.
如图所示,直线AB,CD交于点O,OE平分∠DOB,且∠AOD:∠DOE=3:1,求∠AOC的度数.