题目内容
 已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求sinA的值.
已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.求sinA的值.考点:切线的性质,勾股定理,解直角三角形
专题:计算题
分析:根据切线的性质得∠ACO=90°,由于OA=OB,则根据等腰三角形的性质可得AC=
AB=4,然后在Rt△AOC中利用勾股定理计算出OA=2
,再根据正弦的定义求解.
| 1 |
| 2 |
| 5 |
解答:解:∵AB切⊙O于C,
∴OC⊥AB,
∴∠ACO=90°,
∵OA=OB,
∴AC=BC=
AB=4,
在Rt△AOC中,∵AC=4,OC=2,
∴OA=
=2
,
∴sinA=
=
=
.
∴OC⊥AB,
∴∠ACO=90°,
∵OA=OB,
∴AC=BC=
| 1 |
| 2 |
在Rt△AOC中,∵AC=4,OC=2,
∴OA=
| AC2+OC2 |
| 5 |
∴sinA=
| OC |
| OA |
| 2 | ||
2
|
| ||
| 5 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了等腰三角形的性质和解直角三角形.

练习册系列答案
相关题目
在-3,
,π,0.35中,无理数是( )
| 1 |
| 2 |
| A、-3 | ||
B、
| ||
| C、π | ||
| D、0.35 |
已知抛物线y=x2-x-1,与x轴的一个交点为(m,0),则代数式m2-m+2014的值为( )
| A、2013 | B、2015 |
| C、2014 | D、2010 |
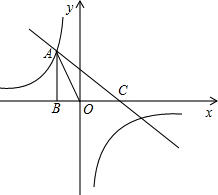 如图,已知反比例函数y1=
如图,已知反比例函数y1= 如图,∠CAB=90°,AD⊥BC,则∠CAD与∠B有何关系?并说明理由.
如图,∠CAB=90°,AD⊥BC,则∠CAD与∠B有何关系?并说明理由.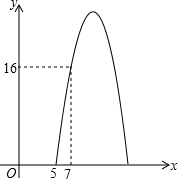 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
 如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E是AD上一点,连接BE,CE,请找出图中所有相等的角,并说明理由.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,点E是AD上一点,连接BE,CE,请找出图中所有相等的角,并说明理由.