题目内容
14．已知正比例函数y=kx（k≠0）的图象经过点（2，1），则k的值为（ ）| A． | 2 | B． | -2 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
分析 直接把（2，1）代入y=kx可求出k的值．
解答 解：把（2，1）代入y=kx得2k=1，解得k=$\frac{1}{2}$．
故选C．
点评 本题考查了一次函数图象上点的坐标特征：一次函数y=kx+b，（k≠0，且k，b为常数）的图象是一条直线．它与x轴的交点坐标是（-$\frac{b}{k}$，0）；与y轴的交点坐标是（0，b）．直线上任意一点的坐标都满足函数关系式y=kx+b．
练习册系列答案
相关题目
4．由线段a，b，c组成的三角形不是直角三角形的是（ ）
| A． | a=15，b=8，c=17 | B． | a=12，b=14，c=15 | C． | a=$\sqrt{41}$，b=4，c=5 | D． | a=7，b=24，c=25 |
如图，直线AB∥CD，MN与AB、CD分别相交于点E、F，若∠AEM=70°，求∠EFD的度数．
9．
已知抛物线y=ax2+bx+c的部分图象如图所示，若y＜0，则x的取值范围是（ ）
已知抛物线y=ax2+bx+c的部分图象如图所示，若y＜0，则x的取值范围是（ ）| A． | -1＜x＜3 | B． | -1＜x＜4 | C． | x＜-1或 x＞4 | D． | x＜-1或 x＞3 |
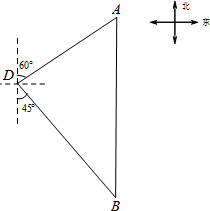钓鱼岛自古以来就是中国的神圣领土，为宣誓主权，我海监船编队奉命在钓鱼岛附近海域进行维权活动．如图，一艘海监船位于钓鱼岛D的北偏东60°方向，与钓鱼岛的距离为16海里的A处，它沿正南方向航行，航行1小时后，发现此时海监船位于钓鱼岛的南偏东45°方向上的B处．
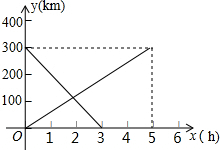甲、乙两车同时从A、B两地相向而行，设两车行驶的时间为x（h），与A地的距离为y（km），y（km）与x（h）关系如图所示：