题目内容
6.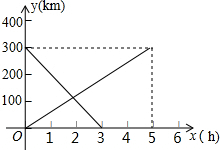 甲、乙两车同时从A、B两地相向而行,设两车行驶的时间为x(h),与A地的距离为y(km),y(km)与x(h)关系如图所示:
甲、乙两车同时从A、B两地相向而行,设两车行驶的时间为x(h),与A地的距离为y(km),y(km)与x(h)关系如图所示:(1)直接写出y甲和y乙的关系式;
(2)甲、乙两车几小时相遇?
(3)当两车距离为100千米时,甲车行驶了多长时间?
(4)当乙车到达A地后立刻按原速度返回,乙能否在甲到达B地前追上甲.
分析 (1)直接运用待定系数法就可以求出y1、y2关于x的函数图关系式;
(2)两车相遇,可得:-100x+300=60x,即可解答;
(3)分两种情况进行讨论:两车相遇前相距100千米和两车相遇后相距100千米,列出方程,即可解答;
(4)当乙车到达A地后立刻按原速度返回,乙车追上甲车时,即100x-300=60x,解得:x=7.5,因为7.5>5,所以乙不能在甲到达B地前追上甲.
解答 解:(1)y甲=60x,y乙=-100x+300;
(2)根据题意得:-100x+300=60x,
解得:x=$\frac{15}{8}$,
答:甲、乙两车$\frac{15}{8}$小时相遇;
(3)根据题意得:
①y甲-y乙=100,即60x-(-100x+300)=100,
解得:x=$\frac{5}{2}$;
②y乙-y甲=100,即-100x+300-60x=100,
解得:x=$\frac{5}{4}$;
答:当两车距离为100千米时,甲车行驶了$\frac{5}{2}$小时或$\frac{5}{4}$小时.
(4)根据题意得:100x-300=60x,
解得:x=7.5,
∵7.5>5,
∴乙不能在甲到达B地前追上甲.
点评 本题考查了分段函数,函数自变量的取值范围,用待定系数法求一次函数、正比例函数的解析式等知识点的运用,综合运用性质进行计算是解此题的关键,通过做此题培养了学生的分析问题和解决问题的能力,注意:分段求函数关系式,题目较好,但是有一定的难度.

练习册系列答案
相关题目
16.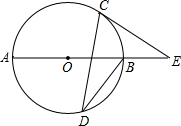 如图,AB是⊙O的直径,C,D 是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则sinE的值为( )
如图,AB是⊙O的直径,C,D 是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则sinE的值为( )
 如图,AB是⊙O的直径,C,D 是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则sinE的值为( )
如图,AB是⊙O的直径,C,D 是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则sinE的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
14.已知正比例函数y=kx(k≠0)的图象经过点(2,1),则k的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
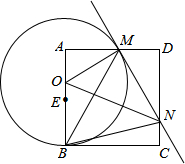 如图,已知正方形ABCD,点E是边AB上一点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM、ON、BM、BN.
如图,已知正方形ABCD,点E是边AB上一点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM、ON、BM、BN.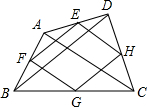 如图,连接四边形ABCD各边中点,得到四边形EFGH,只要添加AC=BD条件,就能保证四边形EFGH是菱形.
如图,连接四边形ABCD各边中点,得到四边形EFGH,只要添加AC=BD条件,就能保证四边形EFGH是菱形. 如图,若直线y=x被双曲线y=$\frac{{k}^{2}}{x}$与双曲线y=$\frac{2{k}^{2}}{x}$在第一象限截得的线段长为2-$\sqrt{2}$.
如图,若直线y=x被双曲线y=$\frac{{k}^{2}}{x}$与双曲线y=$\frac{2{k}^{2}}{x}$在第一象限截得的线段长为2-$\sqrt{2}$.