题目内容
12．观察下列等式：31=3，32=9，33=27，34=81，35=243，36=729，37=2187，…，解答下列问题：31+32+33+34+35+32014=$\frac{{3}^{2015}-3}{2}$．分析 根据题目中的信息，通过变形可以求得31+32+33+34+35+32014的值．
解答 解：设S=31+32+33+34+35+32014，
则3S=32+33+34+35+32014+32015，
∴3S-S=32015-3，
解得，S=$\frac{{3}^{2015}-3}{2}$，
故答案为：$\frac{{3}^{2015}-3}{2}$．
点评 本题考查数字的变化类、有理数的乘方，解题的关键是发现题目中式子的规律，灵活变形，求出所求式子的结果．
练习册系列答案
天天向上口算本系列答案
相关题目
2．
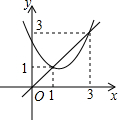如图，已知抛物线y=x2+bx+c与直线y=x交于（1，1）和（3，3）两点，现有以下结论：①b2-4c＞0；
②3b+c+6=0；
③当x2+bx+c＞$\frac{2}{x}$时，x＞2；
④当1＜x＜3时，x2+（b-1）x+c＜0，
其中正确的序号是（ ）
如图，已知抛物线y=x2+bx+c与直线y=x交于（1，1）和（3，3）两点，现有以下结论：①b2-4c＞0；②3b+c+6=0；
③当x2+bx+c＞$\frac{2}{x}$时，x＞2；
④当1＜x＜3时，x2+（b-1）x+c＜0，
其中正确的序号是（ ）
| A． | ①②④ | B． | ②③④ | C． | ②④ | D． | ③④ |
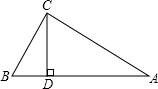如图．在△ABC中，∠ACB=90°．CD是AB边上的高．∠A=30°．想一想：BD与AB有怎样的数量关系．
如图，点M是矩形ABCD的边AD的中点．点P是BC边上一动点，PE⊥MC，PF⊥BM．垂足为E、F．
如图，在△ABC中，∠C=65°，∠ADB=85°，AD是△ABC的角平分线，求∠B的度数．
如图，已知在四边形ABCD中，AD⊥AB，BC⊥AB，∠ADC与∠BCD的平分线交于点E，
如图，D，E分别是AB，AC上的点，已知△AED∽△ABC，AD=4，BD=2，AC=8，求AE的长．
18．已知分式方程$\frac{x}{x-2}$-$\frac{1}{{x}^{2}-4}$=1，去分母后得（ ）
| A． | x（x+2）-1=1 | B． | x（x-2）-1=x2-4 | C． | x（x+2）-1=x2-4 | D． | x-1=x2-4 |