题目内容
2.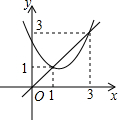 如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2-4c>0;
如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2-4c>0;②3b+c+6=0;
③当x2+bx+c>$\frac{2}{x}$时,x>2;
④当1<x<3时,x2+(b-1)x+c<0,
其中正确的序号是( )
| A. | ①②④ | B. | ②③④ | C. | ②④ | D. | ③④ |
分析 由函数y=x2+bx+c与x轴无交点,可得b2-4c<0;当x=3时,y=9+3b+c=3,3b+c+6=0;利用抛物线和双曲线交点(2,1)得出x的范围;当1<x<3时,二次函数值小于一次函数值,可得x2+bx+c<x,继而可求得答案.
解答 解:∵函数y=x2+bx+c与x轴无交点,
∴b2-4ac<0;
∴b2-4c<0
故①不正确;
当x=3时,y=9+3b+c=3,
即3b+c+6=0;
故②正确;
把(1,1)(3,3)代入y=x2+bx+c,得抛物线的解析式为y=x2-3x+3,
当x=2时,y=x2-3x+3=1,y=$\frac{2}{x}$=1,
抛物线和双曲线的交点坐标为(2,1)
第一象限内,当x>2时,x2+bx+c>$\frac{2}{x}$;
或第三象限内,当x<0时,x2+bx+c>$\frac{2}{x}$;
故③错误;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b-1)x+c<0.
故④正确;
故选C.
点评 本题考查了图象与二次函数系数之间的关系,此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知b<0.则a,a-b,a+b中最大的是( )
| A. | a | B. | a+b | C. | a-b | D. | 以上都不对 |
10.下列说法正确的是( )
| A. | 单项式-$\frac{{x}^{2}}{3}$的系数是-3 | B. | 单项式2πa3的次数是4 | ||
| C. | 多项式x2y2-2x2+3是四次三项式 | D. | 多项式x2-2x+3的项分别是x2、2x、3 |
7.抛物线y=-$\frac{1}{2}$x2+1的顶点坐标是( )
| A. | (0,1) | B. | ($\frac{1}{2}$,1) | C. | (-$\frac{1}{2}$,-1) | D. | (2,-1) |
14.在计算器上,按照下面的程序进行操作:

下表中的x与y分别是输入的6个数及相应的计算结果:
上面操作程序中所按的第三个键应是+,第四个键应是2.

下表中的x与y分别是输入的6个数及相应的计算结果:
| x | -3 | -2 | -1 | 0 | 1 | 2 |
| y | -7 | -4 | -1 | 2 | 5 | 8 |
11.关于函数y=2x2-4x,下列叙述中错误的是( )
| A. | 函数图象经过原点 | B. | 函数图象的最低点是(1,-2) | ||
| C. | 函数图象与x轴的交点为(0,0),(2,0) | D. | 当x>0时,y随x的增大而增大 |
 如图:
如图: