题目内容
4. 如图,已知在四边形ABCD中,AD⊥AB,BC⊥AB,∠ADC与∠BCD的平分线交于点E,
如图,已知在四边形ABCD中,AD⊥AB,BC⊥AB,∠ADC与∠BCD的平分线交于点E,求证:DE⊥CE.
分析 根据已知条件得到AD∥BC,根据平行线的性质得到∠ADC+∠DCB=180°,根据角平分线的定义得到∠EDC=$\frac{1}{2}∠$ADC,∠ECD=$\frac{1}{2}$∠DCB,根据三角形的内角和得到∠E=90°,根据垂直的定义即可得到结论.
解答 证明:∵AD⊥AB,BC⊥AB,
∴AD∥BC,
∴∠ADC+∠DCB=180°,
∵∠ADC与∠BCD的平分线交于点E,
∴∠EDC=$\frac{1}{2}∠$ADC,∠ECD=$\frac{1}{2}$∠DCB,
∴∠EDC+∠ECD=90°,
∴∠E=90°,
∴DE⊥CE.
点评 本题考查了平行线的判定和性质,角平分线的定义,三角形的内角和,正确的识别图形是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
14.在计算器上,按照下面的程序进行操作:

下表中的x与y分别是输入的6个数及相应的计算结果:
上面操作程序中所按的第三个键应是+,第四个键应是2.

下表中的x与y分别是输入的6个数及相应的计算结果:
| x | -3 | -2 | -1 | 0 | 1 | 2 |
| y | -7 | -4 | -1 | 2 | 5 | 8 |
16.对于抛物线y=-$\frac{3}{5}$(x+4)2,下列结论:①抛物线的开口向上;②对称轴为直线x=4;③顶点坐标为(-4,0);④x>-4时,y随x的增大而减小,其中正确结论的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.填表.
| 原数 | -5$\frac{3}{4}$ | -3 | 9.2 | 0 | 4$\frac{1}{3}$ | 7 |
| 相反数 | -5$\frac{3}{4}$ | 3 | -9.2 | 0 | -4$\frac{1}{3}$ | -7 |
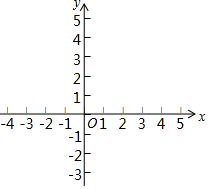 在如图所示的平面直角坐标系中作出y=-x+3和y=2x+6的图象并求两直线的交点坐标.
在如图所示的平面直角坐标系中作出y=-x+3和y=2x+6的图象并求两直线的交点坐标.