题目内容
8.如图,点P,D分别是⊙O上的动点、定点、非直径弦CD⊥直径AB,当点P与点C重合时,易证:∠DPB+∠ACD=90°,在不考虑点P于点B或点D重合的情况下,试解答如下问题:(1)当点P与点A重合时(如图1),∠DPB+∠ACD=90度.
(2)当点P在$\widehat{AC}$上时(如图2),(1)中的结论还成立吗?请给予证明.
(3)当点P在$\widehat{BD}$上时,先写出∠DPB与∠ACD的数量关系,再说明其理由.
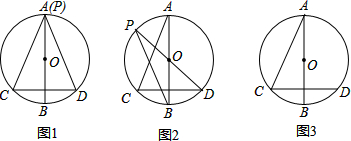
分析 (1)先根据垂径定理得出AC=AD,故可得出∠ACD=∠ADC,∠AED=90°,再由∠DPB+∠ADC=90°即可得出结论;
(2)先根据垂径定理得出$\widehat{BC}$=$\widehat{BD}$,再由∠A+∠ACD=90°即可得出结论;
(3)连接AP,则∠BPD=∠BPA+∠APD,由圆周角定理得出∠BPA=90°,∠ACD=∠APD,进而可得出结论.
解答  解:(1)∵弦CD⊥直径AB,
解:(1)∵弦CD⊥直径AB,
∴CE=DE,∠AED=90°,
∴∠ACD=∠ADC,∠AED=90°.
∵∠DPB+∠ADC=90°,
∴∠DPB+∠ACD=90°.
故答案为:90;
(2)成立.
理由:如图2,∵AB⊥CD,AB是⊙O的直径,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠DPB=∠A.
∵∠A+∠ACD=90°,
∴∠DPB+∠ACD=90°.
(3)∠DPB-∠ACD=90°.
理由:如图3,连接AP,则∠BPD=∠BPA+∠APD.
∵AB是⊙O的直径,
∴∠BPA=90°,∠ACD=∠APD,
∴∠BPD=90°+∠ACD,即∠BPD-∠ACD=90°.
点评 本题考查的是圆的综合题,涉及到圆周角定理及圆心角、弧、弦的关系,难度适中.

练习册系列答案
相关题目
19.下列运算正确的是( )
| A. | $\sqrt{25}=±5$ | B. | $\root{3}{-8}=-2$ | C. | $\sqrt{12}=3\sqrt{2}$ | D. | $3\sqrt{2}-2\sqrt{2}=1$ |
16.甲、乙、丙、丁四位同学参加了10次数学测验,他们测验的平均成绩($\overline{x}$)与方差(S2)如下表所示,那么这四位同学中,成绩较好,且较稳定的是( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 85 | 90 | 90 | 85 |
| S2 | 1.0 | 1.0 | 1.2 | 1.8 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
3.父子二人并排垂站立于游泳池中时,爸爸露出水面的高度是他自身身高的$\frac{1}{3}$,儿子露出水面的高度是他自身身高的$\frac{1}{7}$,父子二人的身高之和为3.2米.若设爸爸的身高为x米,儿子的身高为y米,则可列方程组为( )
| A. | $\left\{\begin{array}{l}{x+y=3.2}\\{(1+\frac{1}{7})x=(1+\frac{1}{3})y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=3.2}\\{(1-\frac{1}{7})x=(1-\frac{1}{3})y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=3.2}\\{\frac{1}{3}x=\frac{1}{7}y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=3.2}\\{(1-\frac{1}{3})x=(1-\frac{1}{7})y}\end{array}\right.$ |
17.超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是77.4分.
| 测试项目 | 创新能力 | 综合知识 | 语言表达 |
| 测试成绩(分数) | 70 | 80 | 92 |
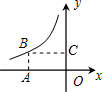 如图,矩形OABC上,点A、C分别在x、y轴上,点B在反比例y=$\frac{k}{x}$位于第二象限的图象上,矩形面积为6,则k的值是( )
如图,矩形OABC上,点A、C分别在x、y轴上,点B在反比例y=$\frac{k}{x}$位于第二象限的图象上,矩形面积为6,则k的值是( )