题目内容
16.甲、乙、丙、丁四位同学参加了10次数学测验,他们测验的平均成绩($\overline{x}$)与方差(S2)如下表所示,那么这四位同学中,成绩较好,且较稳定的是( )| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 85 | 90 | 90 | 85 |
| S2 | 1.0 | 1.0 | 1.2 | 1.8 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
分析 比较平均数的大小可确定乙和丙的成绩较好,然后比较乙和丙的方差即可得到成绩较好,且较稳定的同学.
解答 解:∵乙和丙的平均数比甲和丁的平均数大,
∴乙和丙的成绩较好,
∵S乙2<S丙2,
∴乙的成绩比丙要稳定,
∴这四位同学中,成绩较好,且较稳定的是乙.
故选B.
点评 本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.方差公式是:s2=$\frac{1}{n}$[(x1-x?)2+(x2-x?)2+…+(xn-x?)2].方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
6.计算:|-5+3|的结果是( )
| A. | -8 | B. | 8 | C. | -2 | D. | 2 |
1.2016年我市近9万多名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这1000名考生是总体的一个样本 | B. | 1000名考生是样本容量 | ||
| C. | 每位考生的数学成绩是个体 | D. | 近9万多名考生是总体 |
6.在一个不透明的口袋中装有6个红球,2个绿球,这些球除颜色外无其他差别,从这个袋子中随机摸出一个球,摸到红球的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
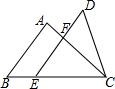 如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是7.
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是7.