题目内容
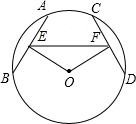 如图所示,⊙O中,AB、CD是弦,点E、F是AB、CD的中点,并且AB=CD.
如图所示,⊙O中,AB、CD是弦,点E、F是AB、CD的中点,并且AB=CD.(1)求证:∠AEF=∠CFE;
(2)若∠EOF=120°,OE=4cm,求EF的长.
考点:垂径定理,勾股定理
专题:
分析:(1)利用同圆或等圆中相等的弦所对的弧、弦心距相等可得EO=FO,进而得到∠OEF=∠OFE,从而可得∠AEO-∠FEO=∠CFO-∠OFE,进而得到∠AEF=∠CFE;
(2)过O作OM⊥EF,根据三角形内角和定理可得∠OEF=30°,再根据直角三角形30°角所对的边等于斜边的一半可得MO长度,利用勾股定理计算出EM长,进而可得EF长.
(2)过O作OM⊥EF,根据三角形内角和定理可得∠OEF=30°,再根据直角三角形30°角所对的边等于斜边的一半可得MO长度,利用勾股定理计算出EM长,进而可得EF长.
解答: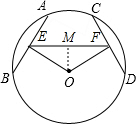 (1)证明:∵点E、F是AB、CD的中点,
(1)证明:∵点E、F是AB、CD的中点,
∴EO⊥AB,FO⊥CD,
∴∠AEO=∠CFO=90°,
∵OE⊥AB于E,OF⊥CD于F,
∴OE和OF是圆的两条弦的弦心距,
∵AB,CD是⊙O的两条弦,AB=CD,
∴EO=FO,
∴∠OEF=∠OFE,
∴∠AEO-∠FEO=∠CFO-∠OFE,
∴∠AEF=∠CFE;
(2)过O作OM⊥EF,
∵∠EOF=120°,
∴∠OEF=30°,
∴MO=
EO=2,
∴EM=
=
=2
,
∴EF=4
.
 (1)证明:∵点E、F是AB、CD的中点,
(1)证明:∵点E、F是AB、CD的中点,∴EO⊥AB,FO⊥CD,
∴∠AEO=∠CFO=90°,
∵OE⊥AB于E,OF⊥CD于F,
∴OE和OF是圆的两条弦的弦心距,
∵AB,CD是⊙O的两条弦,AB=CD,
∴EO=FO,
∴∠OEF=∠OFE,
∴∠AEO-∠FEO=∠CFO-∠OFE,
∴∠AEF=∠CFE;
(2)过O作OM⊥EF,
∵∠EOF=120°,
∴∠OEF=30°,
∴MO=
| 1 |
| 2 |
∴EM=
| EO2-MO2 |
| 16-4 |
| 3 |
∴EF=4
| 3 |
点评:本题考查了垂径定理及勾股定理的知识,解题的关键是正确的将证明弦心距转化为证明两弦相等.

练习册系列答案
相关题目
 一辆卡车装满货物后,它的高比宽多两米,且恰好通过如图所示的隧道,(上部为半圆形).卡车有多高?(结果精确到0.1m).
一辆卡车装满货物后,它的高比宽多两米,且恰好通过如图所示的隧道,(上部为半圆形).卡车有多高?(结果精确到0.1m). 从正方形ABCD的顶点A作∠EAF=45°,交DC于点F,BC于点E.
从正方形ABCD的顶点A作∠EAF=45°,交DC于点F,BC于点E.