题目内容
在Rt△ABC中，∠ACB=90°，∠ABC=60°，D是AC的中点，求tan∠DBC的值．
考点：解直角三角形
专题：
分析：通过解直角三角形得到AC：BC的值；然后通过利用中点的性质和∠DBC的正切的定义进行解答．
解答：
解：∵在Rt△ABC中，∠ACB=90°，∠ABC=60°，
∴tan60°=
=
，则AC=
BC．
又∵D是AC的中点，
∴CD=
AC=
BC．
∴tan∠DBC=
=
=
，即tan∠DBC=
．
解：∵在Rt△ABC中，∠ACB=90°，∠ABC=60°，∴tan60°=
| AC |
| BC |
| 3 |
| 3 |
又∵D是AC的中点，
∴CD=
| 1 |
| 2 |
| ||
| 2 |
∴tan∠DBC=
| CD |
| BC |
| ||||
| BC |
| ||
| 2 |
| ||
| 2 |
点评：本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系．
练习册系列答案
相关题目
下列方程是一元一次方程的是（ ）
A、
| ||
B、
| ||
| C、y2+3y=0 | ||
| D、9x-y=2 |
已知二次函数y=ax2+bx+c的图象如图，则点A（ac，bc）在第
从正方形ABCD的顶点A作∠EAF=45°，交DC于点F，BC于点E．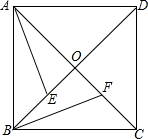
如图，正方形ABCD的对角线交于点O，E、F分别是BO、CO的中点．求证：