题目内容
15.解不等式方程组:(1)$\left\{\begin{array}{l}{\frac{1}{3}(x-2)<2x+1}\\{\frac{x-1}{2}<\frac{1-2x}{3}}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{7-x}{2}-3≤\frac{3+4x}{5}-4}\\{\frac{5}{3}x+5(4-x)≥2(4-x)}\end{array}\right.$
(3)$\left\{\begin{array}{l}{2x-3<4}\\{1-(x-2)<3}\\{1-4x<2x-1}\end{array}\right.$.
分析 首先解出不等式组中的x的取值范围,然后找出它们的公共部分,该公共部分就是不等式组的解集.
解答 解:(1)$\left\{\begin{array}{l}{\frac{1}{3}(x-2)<2x+1}\\{\frac{x-1}{2}<\frac{1-2x}{3}}\end{array}\right.$
解:解不等式①得x>-1,
解不等式②得x<$\frac{5}{7}$,
所以不等式组的解集为-1<x<$\frac{5}{7}$;
(2)$\left\{\begin{array}{l}{\frac{7-x}{2}-3≤\frac{3+4x}{5}-4}\\{\frac{5}{3}x+5(4-x)≥2(4-x)}\end{array}\right.$
解:解不等式①得x≥3,
解不等式②得x≤9,
所以不等式组的解集为3≤x≤9;
(3)$\left\{\begin{array}{l}{2x-3<4}\\{1-(x-2)<3}\\{1-4x<2x-1}\end{array}\right.$
解:解不等式①得x<$\frac{7}{2}$,
解不等式②得x>0,
解不等式③得x>$\frac{1}{3}$.
所以不等式组的解集为$\frac{1}{3}$<x<$\frac{7}{2}$.
点评 本题考查解不等式组,求出不等式公共解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
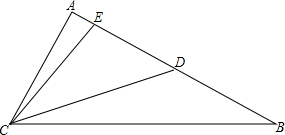 已知∠BCA=80°,AC=AD,BC=BE,求∠ECD的度数.
已知∠BCA=80°,AC=AD,BC=BE,求∠ECD的度数.