题目内容
3.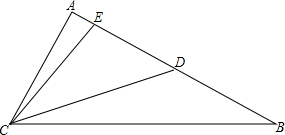 已知∠BCA=80°,AC=AD,BC=BE,求∠ECD的度数.
已知∠BCA=80°,AC=AD,BC=BE,求∠ECD的度数.
分析 由等腰三角形的性质得出∠1=∠4+x,∠3=∠2+x,再运用三角形的外角性质和内角和定理得出∠4+x+∠2+x=100°+∠2+∠4,求出x即可.
解答 解:如图所示: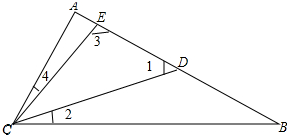 设∠ECD=x,
设∠ECD=x,
∵AC=AD,BC=BE,
∴∠1=∠4+x,∠3=∠2+x,
∵∠1=∠B+∠2,∠3=∠A+∠4,
∴∠1+∠3=∠A+∠B+∠2+∠4,
∵∠BCA=80°,
∴∠A+∠B=100°,
∴∠1+∠3=100°+∠2+∠4,
∴∠4+x+∠2+x=100°+∠2+∠4,
解得:x=50°,
即∠ECD=50°.
点评 本题考查了等腰三角形的性质、三角形的外角性质、三角形内角和定理;熟练掌握等腰三角形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
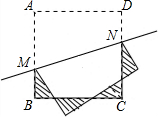 如图,M、N是正方形ABCD中边AB、CD上的点,且AM≠DN,将正方形沿直线MN翻折180°.若正方形ABCD边长为1,则图中阴影部分的四个小三角形的周长和为4.
如图,M、N是正方形ABCD中边AB、CD上的点,且AM≠DN,将正方形沿直线MN翻折180°.若正方形ABCD边长为1,则图中阴影部分的四个小三角形的周长和为4.