题目内容
 直线y=-
直线y=-| 4 |
| 3 |
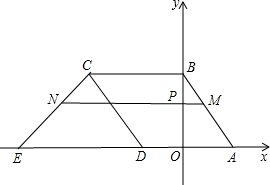
①请直接写出点C、点D的坐标,并求出m的值;
②点P(0,t)是线段OB上的一个动点(点P不与0、B重合),经过点P且平行于x轴的直线交AB于M、交CE于N.设线段MN的长度为d,求d与之间的函数关系式(不要求写自变量的取值范围);
③点P(0,t)是y轴正半轴上的一个动点,为何值时点P、C、D恰好能组成一个等腰三角形?
考点:一次函数综合题
专题:
分析:(1)由直线的解析式可求出A和B点的坐标,再根据菱形的性质即可求出点C、点D的坐标,把点C的坐标代入直线y=x+m即可求出m的值;
(2)设点M的坐标为(xM,t),点N的坐标为(xN,t),首先求出xM=-
t+3,再求出xN=t-9,进而得到d=xM-xN=-
t+3-(t-9)=-
t+12;
(3)由A和B的坐标可求出AB的长,再分三种情况分别讨论求出符合题意的t值即可.
(2)设点M的坐标为(xM,t),点N的坐标为(xN,t),首先求出xM=-
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
(3)由A和B的坐标可求出AB的长,再分三种情况分别讨论求出符合题意的t值即可.
解答:解:(1)∵直线y=-
x+4与x轴交于点A,与y轴交于点B,
∴点A的坐标为(3,0)点B的坐标为(0,4),
∵四边形ABCD是菱形,
∴点C的坐标为(-5,4),点D的坐标为(-2,0),
∵直线y=x+m经过点C,
∴m=9,
(2)∵MN 经过点P(0,t)且平行于x轴,
∴可设点M的坐标为(xM,t),点N的坐标为(xN,t),
∵点M在直线AB上,
直线AB的解析式为y=-
x+4,
∴t=-
xM+4,得xM=-
t+3,
同理点N在直线CE上,直线CE的解析式为y=x+9,
∴t=xN+9,得xN=t-9,
∵MN∥x轴且线段MN的长度为d,
∴d=xM-xN=-
t+3-(t-9)=-
t+12;
(3)∵直线AB的解析式为y=-
x+4,
∴点A 的坐标为(3,0),点B的坐标为(0,4),AB=5,
∵四边形ABCD是菱形,
∴AB=BC=CD=5,
∴点P运动到点B时,△PCD即为△BCD是一个等腰三角形,此时=4;
∵点P(0,t)是y轴正半轴上的一个动点,
∴OP=t,PB=|t-4|,
∵点D的坐标为(-2,0),
∴OD=2,由勾股定理得PD2=OD2+OP2=4+t2,
同理,CP2=BC2+BP2=25+(t-4)2,
当PD=CD=5时,PD2=4+t2=25,
∴t=
(舍负),
当PD=CP时,PD2=CP2,4+t2=25+(t-4)2,
∴t=
,
综上所述,t=4,或t=
,t=
时,△PCD均为等腰三角形.
| 4 |
| 3 |
∴点A的坐标为(3,0)点B的坐标为(0,4),
∵四边形ABCD是菱形,
∴点C的坐标为(-5,4),点D的坐标为(-2,0),
∵直线y=x+m经过点C,
∴m=9,
(2)∵MN 经过点P(0,t)且平行于x轴,
∴可设点M的坐标为(xM,t),点N的坐标为(xN,t),
∵点M在直线AB上,
直线AB的解析式为y=-
| 4 |
| 3 |
∴t=-
| 4 |
| 3 |
| 3 |
| 4 |
同理点N在直线CE上,直线CE的解析式为y=x+9,
∴t=xN+9,得xN=t-9,
∵MN∥x轴且线段MN的长度为d,
∴d=xM-xN=-
| 3 |
| 4 |
| 7 |
| 4 |
(3)∵直线AB的解析式为y=-
| 4 |
| 3 |
∴点A 的坐标为(3,0),点B的坐标为(0,4),AB=5,

∵四边形ABCD是菱形,
∴AB=BC=CD=5,
∴点P运动到点B时,△PCD即为△BCD是一个等腰三角形,此时=4;
∵点P(0,t)是y轴正半轴上的一个动点,
∴OP=t,PB=|t-4|,
∵点D的坐标为(-2,0),
∴OD=2,由勾股定理得PD2=OD2+OP2=4+t2,
同理,CP2=BC2+BP2=25+(t-4)2,
当PD=CD=5时,PD2=4+t2=25,
∴t=
| 21 |
当PD=CP时,PD2=CP2,4+t2=25+(t-4)2,
∴t=
| 37 |
| 8 |
综上所述,t=4,或t=
| 21 |
| 37 |
| 8 |
点评:本题是一次函数与菱形相结合的问题,用到的知识点有勾股定理的运用,等腰三角形的判定和性质,其中在图形中渗透运动的观点是中考中经常出现的问题.

练习册系列答案
相关题目
下列说法中错误的是( )
| A、过直线外一点有且只有一条直线平行于已知直线 |
| B、两条直线平行,同旁内角互补 |
| C、在同一平面内不相交的两条直线叫做平行线 |
| D、有公共顶点,有一条公共边且互补的两个角叫邻补角 |
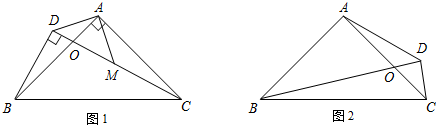
 如图,D为△ABC的AB边的中点,过点D作AB的垂线交BC于点E,连接AE,若AC=8cm,BC=12cm,则△ACE的周长为( )
如图,D为△ABC的AB边的中点,过点D作AB的垂线交BC于点E,连接AE,若AC=8cm,BC=12cm,则△ACE的周长为( )| A、20cm | B、18cm |
| C、15cm | D、12cm |
 完成推理填空:
完成推理填空: