Question

8． 如图，在菱形ABCD中，∠A=60°，点P、Q分别在边AB、BC上，且AP=BQ．
（1）求证：△BDQ≌△ADP；
（2）已知AD=3，AP=2，求PQ．

Answer 1

分析 （1）由四边形ABCD是菱形，可得AD=AB，∠ABD=∠CBD=$\frac{1}{2}$∠ABC，AD∥BC，又由∠A=60°，易得△ABD是等边三角形，然后由SAS即可得△BDQ≌△ADP；
（2）首先过点Q作QE⊥AB，交AB的延长线于E，然后由三角函数的性质，即可求得PE与QE的长，又由勾股定理，即可求得PQ的长．

解答 （1）证明：∵四边形ABCD是菱形，
∴AD=AB，∠ABD=∠CBD=$\frac{1}{2}$∠ABC，AD∥BC，
∵∠A=60°，
∴△ABD是等边三角形，∠ABC=120°，
∴AD=BD，∠CBD=∠A=60°，
∵AP=BQ，
∴△BDQ≌△ADP（SAS）；

（2）解：过点Q作QE⊥AB，交AB的延长线于E，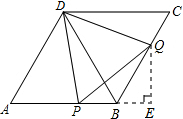
∵BQ=AP=2，
∵AD∥BC，
∴∠QBE=60°，
∴QE=QB•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$，BE=QB•cos60°=2×$\frac{1}{2}$=1，
∵AB=AD=3，
∴PB=AB-AP=3-2=1，
∴PE=PB+BE=2，
∴在Rt△PQE中，PQ=$\sqrt{P{E}^{2}+Q{E}^{2}}$=$\sqrt{7}$．

点评 此题考查了菱形的性质与勾股定理、三角函数的性质．此题难度适中，解题的关键是数形结合思想的应用．