题目内容
当两圆相切时,圆心距为12cm,若两圆半径之差为4cm,则这两圆的半径分别为 .
考点:圆与圆的位置关系
专题:
分析:根据两圆相切圆心距为12cm得到两圆的半径之和,然后根据半径之差求得两圆的半径即可.
解答:解:设两圆的半径分别为R和r,
∵两圆相切时,圆心距为12cm,
∴R+r=12,
∵两圆半径之差为4cm,
∴
,
解得:R=8,r=4,
故答案为8,4.
∵两圆相切时,圆心距为12cm,
∴R+r=12,
∵两圆半径之差为4cm,
∴
|
解得:R=8,r=4,
故答案为8,4.
点评:本题考查了圆与圆的位置关系,解题的关键是根据两圆相切得到两圆的半径之和,难度不大.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
某运动员投一次篮投中的概率为0.8,则下列说法正确的是( )
| A、该运动员投10次篮,必有8次投中 |
| B、该运动员投10次篮,恰好8次投中的可能性很大 |
| C、该运动员投1000次篮,约有800次投中 |
| D、该运动员投1000次篮,必有800次投中 |
 如图所示,AD是△ABC的高,E、F分别是AB的、AC的中点.求证:△DFE∽△ABC.
如图所示,AD是△ABC的高,E、F分别是AB的、AC的中点.求证:△DFE∽△ABC. 如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,如果CD=3DA=3,那么CC′=
如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,如果CD=3DA=3,那么CC′=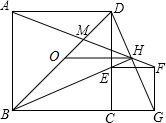 如图,ABCD、CEFG是正方形,E在CD上,且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,则OH=
如图,ABCD、CEFG是正方形,E在CD上,且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,则OH=