Question

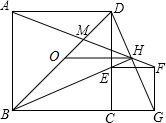如图，ABCD、CEFG是正方形，E在CD上，且BE平分∠DBC，O是BD中点，直线BE、DG交于H．BD，AH交于M，连接OH，则OH=

 

，BM=

 

．

Answer 1

考点：四点共圆

专题：

分析：易得△BCE≌△DCG，得到∠1=∠2，B，C，H，D四点共圆，得出OH=

1

2

BD=

2

2

AB，由E关于BD的对称E′，得到△BEE′是等腰三角形，BM⊥E′E于M，由角平分线到角两边的距离相等得出BM=AB．

解答：解：如图，

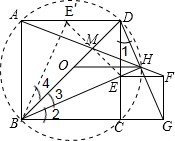
∵BC=DC，EC=CG，∠BCE=∠DCG，
在△BCE和△DCG中，

BC=DC ∠BCE=∠DCG EC=CG

，
∴△BCE≌△DCG（SAS），
∴∠1=∠2，
∴B，C，H，D四点共圆，
∴OH=

1

2

BD=

2

2

AB，
∵E关于BD的对称E′，
∵∠3=∠4，BE=BE′，
∴△BEE′是等腰三角形，
∴BM⊥E′E于M，
∴BM=AB．
故答案为：

2

2

AB，AB．

点评：本题主要考查了四点共圆，解题的关键是B，C，H，D四点共圆．