题目内容
18.解答题(用配方法解一元二次方程)(1)x2-2x-1=0
(2)y2-6y+6=0
(3)5x2+4x=1.
分析 (1)、(2)把常数项移项后,在左右两边同时加上一次项系数的一半的平方.
(3)化二次项系数为1,在左右两边同时加上一次项系数的一半的平方.
解答 解:(1)x2-2x-1=0,
x2-2x=1,
x2-2x+1=1+1,
(x-1)2=2,
x-1=±$\sqrt{2}$,
解得x=1±$\sqrt{2}$;
(2)y2-6y+6=0,
y2-6y=-6,
y2-6y+9=-6+9,
(y-3)2=3,
y-3=±$\sqrt{3}$,
解得y=3±$\sqrt{3}$;
(3)5x2+4x=1,
x2+$\frac{4}{5}$x=$\frac{1}{5}$,
x2+$\frac{4}{5}$x+$\frac{4}{25}$=$\frac{1}{5}$+$\frac{4}{25}$,
(x+$\frac{2}{5}$)2=$\frac{9}{25}$,
x+$\frac{2}{5}$=±$\frac{3}{5}$,
解得x1=$\frac{1}{5}$,x2=-1.
点评 本题考查了配方法解一元二次方程.配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
相关题目
20.△ABC中,∠C=90°,AB=5,BC=4,以A为圆心,以3为半径画圆,点B与⊙A的位置关系是( )
| A. | 在⊙O外 | B. | 在⊙O上 | C. | 在⊙O内 | D. | 不能确定 |
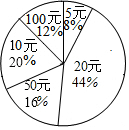 在一次救灾捐款活动中,某班50名同学人人拿出自己的零花线,有捐5元、10元、20元的,还有捐50元和100元的.如图所示的统计图反映了不同捐款数的人数比例,那么该班同学捐款的平均数、众数和中位数分别是31.2元、20元、20元.
在一次救灾捐款活动中,某班50名同学人人拿出自己的零花线,有捐5元、10元、20元的,还有捐50元和100元的.如图所示的统计图反映了不同捐款数的人数比例,那么该班同学捐款的平均数、众数和中位数分别是31.2元、20元、20元.