已知x=$\frac{1}{2-\sqrt{3}}$.y=$\frac{1}{2+\sqrt{3}}$.求x2+xy+y2的值．题目和参考答案——青夏教育精英家教网—

题目内容

20．已知x=$\frac{1}{2-\sqrt{3}}$，y=$\frac{1}{2+\sqrt{3}}$，求x²+xy+y²的值．

分析分别将x、y化简，然后代入代数式求值即可．

解答解：∵x=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$，y=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$，
∴原式=（x+y）²-xy
=（2+$\sqrt{3}$+2-$\sqrt{3}$）²-（2+$\sqrt{3}$）（2-$\sqrt{3}$）
=16-1
=15．

点评本题考查了二次根式的化简求值的知识，解题的关键是能够对x、y进行化简，难度不大．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

相关题目

17．已知x²-4y+y²+8x+20=0，求x、y的值．

18．不等式组$\left\{\begin{array}{l}{2x+1＞0}\\{\frac{3x-1}{2}≤\frac{2x+1}{3}}\end{array}\right.$的所有整数解是0，1．

8．研究下列算式，你会发现有什么规律？
1×3+1=4=2²，
2×4+1=9=3²，
3×5+1=16=4²，
4×6+1=25=5²，
…
将你发现的规律用字母n表示出来，并利用上述规律计算下列算式：
（1）99×101+1；
（2）2005×2007+1．

15．计算下列各题：
（1）$\sqrt{8}×\sqrt{\frac{1}{2}}+{（\sqrt{2}）^0}$
（2）$（\sqrt{48}-4\sqrt{\frac{1}{8}}）-（3\sqrt{\frac{1}{3}}-2\sqrt{0.5}）$
（3）${（\frac{1}{{\sqrt{6}}}）^{-2}}+\sqrt{20}÷\sqrt{5}$
（4）${（2-\sqrt{3}）^{2013}}•{（2+\sqrt{3}）^{2014}}-2|{-\frac{{\sqrt{3}}}{2}}|-{（-\sqrt{3}）^0}$．

5．将下列多项式因式分解．
（1）9x²-y²-4y-4
（2）x²-5x+6
（3）x⁴-16
（4）（2a-b）²+8ab．

12．服装厂准备生产某种样式的服装40000套，分黑色和彩色两种．
（1）若生产黑色服装的套数不多于彩色服装套数的$\frac{1}{4}$，问最多生产多少套黑色服装？
（2）目前工厂有100名工人，平均每人生产400套，由于展品会上此种样式服装大受欢迎，工厂计划增加产量；由于条件发生变化，人均生产套数将减少1.25a%（20＜a＜30），要使生产总量增加10%，则工人需增加2.4a%，求a的值．

9．

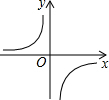已知函数$y=\frac{m}{x}$图象如图，以下结论，其中正确有（　　）个：
①m＜0；
②在每个分支上y随x的增大而增大；
③若A（-1，a），点B（2，b）在图象上，则a＜b
④若P（x，y）在图象上，则点P₁（-x，-y）也在图象上．

10．已知a=-（0.2）²，b=-2²，c=（-$\frac{1}{2}$）^-2，d=（-$\frac{1}{2}$）⁰，则比较a、b、c、d的大小结果是（　　）

试题分类