题目内容
5.将下列多项式因式分解.(1)9x2-y2-4y-4
(2)x2-5x+6
(3)x4-16
(4)(2a-b)2+8ab.
分析 (1)将后三项分组利用完全平方公式以及平方差公式分解因式得出即可;
(2)利用十字相乘法分解因式得出即可;
(3)利用平方差公式法分解因式得出即可;
(4)首先去括号,进而利用完全平方公式进行分解即可.
解答 解:(1)9x2-y2-4y-4
=9x2-(y+2)2
=(3x+y+2)(3x-y-2);
(2)x2-5x+6=(x-3)(x-2);
(3)x4-16
=(x2+4)(x2-4)
=(x2+4)(x-2)(x+2);
(4)(2a-b)2+8ab
=4a2+b2-4ab+8ab
=4a2+b2+4ab
=(2a+b)2.
点评 此题主要考查了分组分解法因式分解以及公式法分解因式和十字相乘法分解因式,正确分组得出是解题关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
13.下列计算正确的是( )
| A. | $4\sqrt{3}-3\sqrt{3}=1$ | B. | $\sqrt{2}+\sqrt{5}=\sqrt{5}$ | C. | $2\sqrt{\frac{1}{2}}=2$ | D. | $3\sqrt{2}+2\sqrt{2}=5\sqrt{2}$ |
10.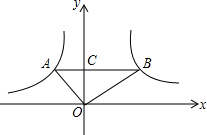 如图,在直角坐标系中,O为坐标原点,函数y1=$\frac{{k}_{1}}{x}$(x<0)和y2=$\frac{{k}_{2}}{x}$(x>0)的图象上,分别有A、B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=$\frac{1}{2}$,S△BOC=$\frac{9}{2}$,则线段AB的长度为( )
如图,在直角坐标系中,O为坐标原点,函数y1=$\frac{{k}_{1}}{x}$(x<0)和y2=$\frac{{k}_{2}}{x}$(x>0)的图象上,分别有A、B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=$\frac{1}{2}$,S△BOC=$\frac{9}{2}$,则线段AB的长度为( )
 如图,在直角坐标系中,O为坐标原点,函数y1=$\frac{{k}_{1}}{x}$(x<0)和y2=$\frac{{k}_{2}}{x}$(x>0)的图象上,分别有A、B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=$\frac{1}{2}$,S△BOC=$\frac{9}{2}$,则线段AB的长度为( )
如图,在直角坐标系中,O为坐标原点,函数y1=$\frac{{k}_{1}}{x}$(x<0)和y2=$\frac{{k}_{2}}{x}$(x>0)的图象上,分别有A、B两点,若AB∥x轴且交y轴于点C,且OA⊥OB,S△AOC=$\frac{1}{2}$,S△BOC=$\frac{9}{2}$,则线段AB的长度为( )| A. | 3$\sqrt{3}$ | B. | $\frac{10}{3}$$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 4 |
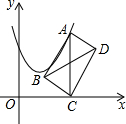 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为1.
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为1.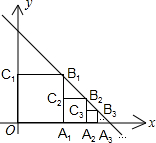 正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0).
正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0).