题目内容
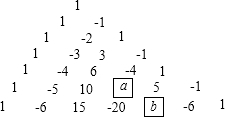
8.研究下列算式,你会发现有什么规律?1×3+1=4=22,
2×4+1=9=32,
3×5+1=16=42,
4×6+1=25=52,
…
将你发现的规律用字母n表示出来,并利用上述规律计算下列算式:
(1)99×101+1;
(2)2005×2007+1.
分析 根据所给数列可发现:n(n+2)+1=(n+1)2,由此可以得出结论.
解答 解:∵1×3+1=4=22,2×4+1=9=32,3×5+1=16=42,4×6+1=25=52,…、
∴可发现:n(n+2)+1=(n+1)2(n为正整数).
(1)99×101+1=(99+1)2=1002=10000=104;
(2)2005×2007+1=(2005+1)2=20062.
点评 本题主要考查的是数列的排列规律,根据所给数列发现一般性规律是解决此类问题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
13.下列计算正确的是( )
| A. | $4\sqrt{3}-3\sqrt{3}=1$ | B. | $\sqrt{2}+\sqrt{5}=\sqrt{5}$ | C. | $2\sqrt{\frac{1}{2}}=2$ | D. | $3\sqrt{2}+2\sqrt{2}=5\sqrt{2}$ |
18.x7等于( )
| A. | (-x2)•x5 | B. | (-x)3x4 | C. | (-x2)•(-x5) | D. | (-x)(-x)6 |

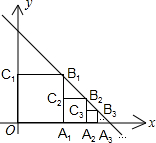 正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0).
正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0).