题目内容
18.不等式组$\left\{\begin{array}{l}{2x+1>0}\\{\frac{3x-1}{2}≤\frac{2x+1}{3}}\end{array}\right.$的所有整数解是0,1.分析 先求出两个不等式的解集,再求其公共解,然后写出范围内的整数即可.
解答 解:$\left\{\begin{array}{l}{2x+1>0①}\\{\frac{3x-1}{2}≤\frac{2x+1}{3}②}\end{array}\right.$,
解不等式①得,x>-$\frac{1}{2}$,
解不等式②得,x≤1,
所以不等式组的解集为-$\frac{1}{2}<$x≤1,
所以原不等式组的整数解是0,1.
故答案为:0,1.
点评 本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
相关题目
13.在天水市汉字听写大赛中,10名学生得分情况如表
那么这10名学生所得分数的中位数和众数分别是( )
| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 85和82.5 | B. | 85.5和85 | C. | 85和85 | D. | 85.5和80 |
 如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件∠BAD=90°,使四边形ABCD是正方形(填一个即可).
如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件∠BAD=90°,使四边形ABCD是正方形(填一个即可).
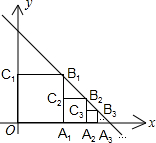 正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0).
正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0).
 如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为( )
如图,在等边三角形ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为( )