题目内容
1.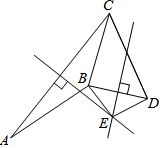 已知:如图,AB=CD,线段AC的垂直平分线与线段BD的垂直平分线相交于点E.求证:∠ABE=∠CDE.
已知:如图,AB=CD,线段AC的垂直平分线与线段BD的垂直平分线相交于点E.求证:∠ABE=∠CDE.
分析 连接AE、CE,根据垂直平分线的性质得出AE=CE,BE=DE,根据SSS推出△ABE≌△CDE即可.
解答  证明:连接AE、CE,
证明:连接AE、CE,
∵AC、BD的垂直平分线相交于E,
∴AE=CE,BE=DE,
在△ABE和△CDE中,$\left\{\begin{array}{l}{AB=CD}\\{AE=CE}\\{BE=DE}\end{array}\right.$,
∴△ABE≌△CDE(SSS),
∴∠ABE=∠CDE.
点评 本题考查了垂直平分线的性质和全等三角形的性质和判定的应用,关键是推出△ABE≌△CDE.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,说明它是假命题的反例可以是( )
| A. | ∠1=50°,∠2=40° | B. | ∠1=50°,∠2=50° | C. | ∠1=40°,∠2=40° | D. | ∠1=∠2=45° |
6.下列计算正确的是( )
| A. | 4x-9x+6x=-x | B. | a-a=0 | C. | x3-x2=x | D. | xy-2xy=3xy |
13.某商场为提高彩电销售人员的积极性,制订了新的工资分配方案,方案规定:每位销售人员的工资总额=基本工资+奖励工资,每位销售人员的月销售额为20000元,在销售定额内,得基本工资2000元.超过销售定额,超过部分的销售额按相应比例作为奖励工资,奖励工资发放比例表1所示.
表1:
表2:
(1)已知销售员甲本月领到的工资总额为2900元,请问销售员甲本月销售额是多少元?
(2)依法纳税是每个公民应尽的义务.根据我国税法规定,全月工资总额不超过3500元不必缴纳个人所得税;超过3500元的部分为“全月应纳税所得额”,表2是缴纳个人所得税率表.若销售员乙本月销售A、B两种型号的彩电15台,缴纳个人所得税后实际得到的工资为4858元.又知A型彩电的销售价为每台400元,B型彩电的销售价为每台6000元,请问销售员乙本月销售A型彩电多少台?
表1:
| 销售额 | 奖励工资比例 |
| 超过20000元但不超过30000部分 | 3% |
| 超过30000元但不超过50000部分 | 5% |
| 50000元以上的部分 | 8% |
| 全月应纳税所得额 | 税率 |
| 不超过1500元部分 | 3% |
| 超过1500元至4500元部分 | 10% |
| … | … |
(2)依法纳税是每个公民应尽的义务.根据我国税法规定,全月工资总额不超过3500元不必缴纳个人所得税;超过3500元的部分为“全月应纳税所得额”,表2是缴纳个人所得税率表.若销售员乙本月销售A、B两种型号的彩电15台,缴纳个人所得税后实际得到的工资为4858元.又知A型彩电的销售价为每台400元,B型彩电的销售价为每台6000元,请问销售员乙本月销售A型彩电多少台?
10.下列计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (b-a)2=b2-2ab+a2 | C. | (a+2b)(a-2b)=a2-2b2 | D. | (a-b)2=a2-2ab-b2 |
11.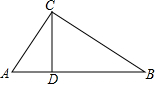 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )
 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知BC=a,∠A=α,则下列结论错误的是( )| A. | BD=a•sinα | B. | AD=$\frac{a•sinα}{tanα}$ | C. | AC=$\frac{a}{sinα}$ | D. | CD=a•cosα |
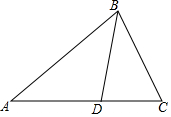 已知:如图,在△ABC中,D是AC上一点,$\frac{CB}{CD}$=$\frac{CA}{CB}$=$\frac{3}{2}$,△BCD的周长是24cm.
已知:如图,在△ABC中,D是AC上一点,$\frac{CB}{CD}$=$\frac{CA}{CB}$=$\frac{3}{2}$,△BCD的周长是24cm. 如图,已知AB=BC,要使△ABD≌△CBD,还需要加一个条件,你添加的条件是AD=CD(答案不唯一).(只需写一个,不添加辅助线)
如图,已知AB=BC,要使△ABD≌△CBD,还需要加一个条件,你添加的条件是AD=CD(答案不唯一).(只需写一个,不添加辅助线)