题目内容
13.三个互不相等的有理数,既可以表示为1、a+b、a的形式,又可以表示为0、$\frac{b}{a}$、b的形式,则a2014+b2015的值2.分析 根据题意可知a+b=0,从而可知b=1,a=-1,然后代入计算即可.
解答 解:根据题意可知:1、a+b、a中有一个为0,
∵a≠0,
∴a+b=0.
∴$\frac{b}{a}$=-1.
∴a=-1,b=1.
∴原式=(-1)2014+12015=1+1=2.
故答案为:2.
点评 本题主要考查的是求代数式的值,求得a、b的值是解题的关键.

练习册系列答案
相关题目
8.若a,b互为相反数,c,d互为倒数,|m|=2,则$\frac{a+b}{{m}^{3}+1}$+m-cd的值为( )
| A. | 4 | B. | -3 | C. | 1 | D. | -3或1 |
18.A、B两个动点在数轴上做匀速运动,它们的运动时间以及位置记录如下.
(1)根据题意,填写下列表格;
(2)A、B两点能否相遇?如果相遇,求相遇时的时刻及在数轴上的位置;如果不能相遇,请说明理由;
(3)A、B两点能否相距18个单位长度?如果能,求相距18个单位长度的时刻;如不能,请说明理由.
(1)根据题意,填写下列表格;
| 时间(s) | 0 | 5 | 7 | x |
| A点位置 | 19 | -1 | -9 | -4x+19 |
| B点位置 | -8 | 17 | 27 | 5x-8 |
(3)A、B两点能否相距18个单位长度?如果能,求相距18个单位长度的时刻;如不能,请说明理由.
 如图,一条公路的转弯处是一段圆弧AB.
如图,一条公路的转弯处是一段圆弧AB.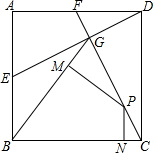 如图,正方形ABCD中,点E是AB的中点,连接DE,在DE上取一点G,连接BG,使BG=BC,连接CG并延长与AD交于点F,在CG上取一动点P(不与点C,点G重合),过点P分别作BG和BC的垂线,垂足分别为点M,点N.若四边形AEGF的面积是$\frac{4}{5}$,则PM+PN的值为$\frac{8}{5}$.
如图,正方形ABCD中,点E是AB的中点,连接DE,在DE上取一点G,连接BG,使BG=BC,连接CG并延长与AD交于点F,在CG上取一动点P(不与点C,点G重合),过点P分别作BG和BC的垂线,垂足分别为点M,点N.若四边形AEGF的面积是$\frac{4}{5}$,则PM+PN的值为$\frac{8}{5}$.