题目内容
7.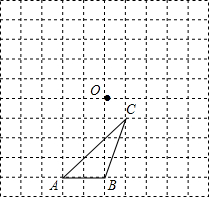 如图所示,△ABC与点O在10×10的网格中的位置如图所示
如图所示,△ABC与点O在10×10的网格中的位置如图所示(1)画出△ABC绕点O逆时针旋转90°后的图形;
(2)画出△ABC绕点O逆时针旋转180°后的图形;
(2)若⊙M能盖住△ABC,则⊙M的半径最小值为$\frac{3\sqrt{2}}{2}$.
分析 (1)利用网格特点和旋转的性质画出点A、B、C的对应点A′、B′、C′,于是可得到△A′B′C′;
(2)利用网格特点和中心对称的性质画出点A、B、C的对应点A″、B″、C″,于是可得到△A″B″C″;
(3)以AC为直径的圆为能盖住△ABC的最小圆,然后利用勾股定理计算出AC即可.
解答 解:(1)如图,△A′B′C′为所作;
(2)如图,△A″B″C″为所求;
(3)如图,当点M为AC的中点时,此时⊙M是能盖住△ABC的最小的圆,⊙M的半径为$\frac{3\sqrt{2}}{2}$.
故答案为$\frac{3\sqrt{2}}{2}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了三角形的外心.

练习册系列答案
相关题目
18.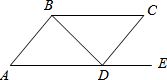 如图,点E在AD的延长线上,下列条件中能使AB∥CD的是( )
如图,点E在AD的延长线上,下列条件中能使AB∥CD的是( )
 如图,点E在AD的延长线上,下列条件中能使AB∥CD的是( )
如图,点E在AD的延长线上,下列条件中能使AB∥CD的是( )| A. | ∠ABD=∠CDB | B. | ∠ADB=∠CBD | C. | ∠C=∠CDE | D. | ∠C+∠ADC=180° |
19.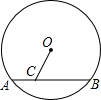 如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )
如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )
 如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )
如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )| A. | $\sqrt{13}$ | B. | 3 | C. | 4 | D. | 2$\sqrt{3}$ |
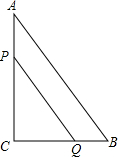 如图,在Rt△ACB中,AC=8m,BC=6m,点P、Q同时由C、B两点出发分别沿CA、BC向点A、C匀速移动,它们的速度分别是2米/秒、1米/秒,问几秒后△PCQ与△ACB相似?
如图,在Rt△ACB中,AC=8m,BC=6m,点P、Q同时由C、B两点出发分别沿CA、BC向点A、C匀速移动,它们的速度分别是2米/秒、1米/秒,问几秒后△PCQ与△ACB相似?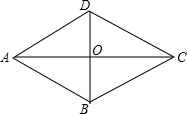 如图,菱形ABCD的周长为48cm,它的一条对角线BD长12cm.
如图,菱形ABCD的周长为48cm,它的一条对角线BD长12cm. 求出下列图形中的x值.
求出下列图形中的x值.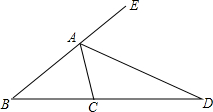 如图,已知△ABC中,AD是△ABC外角平分线,交BC延长线于D,求证:$\frac{AB}{AC}$=$\frac{BD}{DC}$.
如图,已知△ABC中,AD是△ABC外角平分线,交BC延长线于D,求证:$\frac{AB}{AC}$=$\frac{BD}{DC}$.