题目内容
17.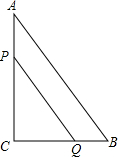 如图,在Rt△ACB中,AC=8m,BC=6m,点P、Q同时由C、B两点出发分别沿CA、BC向点A、C匀速移动,它们的速度分别是2米/秒、1米/秒,问几秒后△PCQ与△ACB相似?
如图,在Rt△ACB中,AC=8m,BC=6m,点P、Q同时由C、B两点出发分别沿CA、BC向点A、C匀速移动,它们的速度分别是2米/秒、1米/秒,问几秒后△PCQ与△ACB相似?
分析 设x秒后△PCQ与△ACB相似;则CP=2x,BQ=x,CQ=6-x.当$\frac{CP}{CB}=\frac{CQ}{CA}$,或$\frac{CP}{CA}=\frac{CQ}{CB}$时,△PCQ与△ACB相似,解方程即可.
解答 解:设x秒后△PCQ与△ACB相似.
由题知,CP=2x,BQ=x,CQ=6-x.
∵∠C=∠C,
当$\frac{CP}{CB}=\frac{CQ}{CA}$,或$\frac{CP}{CA}=\frac{CQ}{CB}$,△PCQ与△ACB相似.
∴$\frac{2x}{6}=\frac{6-x}{8}$,或$\frac{2x}{8}=\frac{6-x}{6}$,
解得:x=$\frac{18}{11}$,或x=$\frac{12}{5}$;
∴$\frac{18}{11}$秒或$\frac{12}{5}$秒后△PCQ与△ACB相似.
点评 本题考查了相似三角形的判定;熟练掌握相似三角形的判定方法,由两边成比例得出方程是解决问题的关键.

练习册系列答案
相关题目
8.已知A、B两点的坐标分别为(-2,3)和(2,3),则下面四个结论:①A、B关于x轴对称;②A、B关于y轴对称;③在x轴上存在一点P,当PA+PB的值最小时,点P坐标为(0.5,0);④A、B之间的距离为4,其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.已知点A(a+1,1),点B(3,-1),且A、B关于x轴对称,则a的值为( )
| A. | -3 | B. | 3 | C. | -2 | D. | 2 |

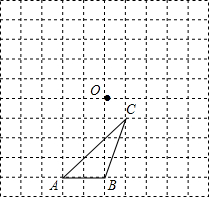 如图所示,△ABC与点O在10×10的网格中的位置如图所示
如图所示,△ABC与点O在10×10的网格中的位置如图所示