题目内容
18.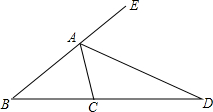 如图,已知△ABC中,AD是△ABC外角平分线,交BC延长线于D,求证:$\frac{AB}{AC}$=$\frac{BD}{DC}$.
如图,已知△ABC中,AD是△ABC外角平分线,交BC延长线于D,求证:$\frac{AB}{AC}$=$\frac{BD}{DC}$.
分析 作DF∥AC交AE于F,如图,由AD是△ABC外角∠EAC的平分线得到∠1=∠2,由AC∥DF得∠2=∠3,则∠1=∠3,所以FA=FD,再根据平行线分线段成比例,
由AC∥DF得到AC:DF=BC:BD,AB:AF=BC:CD,利用比例的性质得到AC•BD=DF•BC,AB•CD=AF•BC,所以AC•BD=AB•CD,然后根据比例性质即可得到结论.
解答 证明:作DF∥AC交AE于F,如图,
∵AD是△ABC外角∠EAC的平分线,
∴∠1=∠2,
∵AC∥DF,
∴∠2=∠3,
∴∠1=∠3,
∴FA=FD,
∵AC∥DF,
∴AC:DF=BC:BD,AB:AF=BC:CD,
∴AC•BD=DF•BC,AB•CD=AF•BC,
而FA=FD,
∴AC•BD=AB•CD,
∴AB:AC=BD:DC.
点评 本题考查了平行线分线段成比例,角平分线的定义,平行线的性质,熟练掌握平行线分线段成比例定理是解题的关键.

练习册系列答案
相关题目
10.如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1面积为S1,△B3D2C2面积为S2,…,△Bn+1DnCn面积为Sn,则S2013等于( )


| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2013\sqrt{3}}{2014}$ | D. | $\frac{2014\sqrt{3}}{2015}$ |
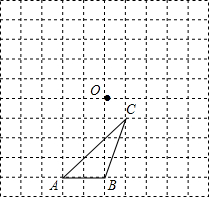 如图所示,△ABC与点O在10×10的网格中的位置如图所示
如图所示,△ABC与点O在10×10的网格中的位置如图所示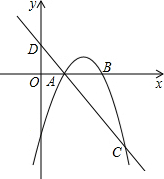 如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).
如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).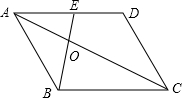 如图,在?ABCD中,点E是AD的中点,连接AC、BE相交于点O,则S△AOE:S△AOB=$\frac{1}{2}$.
如图,在?ABCD中,点E是AD的中点,连接AC、BE相交于点O,则S△AOE:S△AOB=$\frac{1}{2}$.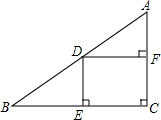 如图,△ABC中,∠C=90°,D是AB上一点,过点D作DE⊥BC于E,DF⊥AC于F,AC=6,BC=8.
如图,△ABC中,∠C=90°,D是AB上一点,过点D作DE⊥BC于E,DF⊥AC于F,AC=6,BC=8.