题目内容
15.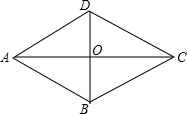 如图,菱形ABCD的周长为48cm,它的一条对角线BD长12cm.
如图,菱形ABCD的周长为48cm,它的一条对角线BD长12cm.(1)求菱形的每一个内角的度数.
(2)求菱形另一条对角线AC的长.
分析 (1)利用已知条件和菱形的性质已知△ABD是等边三角形,所以可求出∠BAD的度数,进而可求出菱形其他内角的度数;
(2)利用勾股定理可求出OA的长,因为AC=2OA,所以AC可求出.
解答 解:(1)在菱形ABCD中,AB=AD=BD=12,
∴△ABD为等边三角形,
∴∠BAD=∠BCD=60°,
∴∠ABC=∠ADC=120°;
(2)在菱形ABCD中,AC⊥BD,OD=6,
∴OA=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,
∴AC=2OA=12$\sqrt{3}$cm.
点评 本题考查了菱形的性质、等边三角形的判定和性质以及勾股定理的运用,解题的关键是熟记各种特殊几何图形的判定及其性质.

练习册系列答案
相关题目
5.已知点A(a+1,1),点B(3,-1),且A、B关于x轴对称,则a的值为( )
| A. | -3 | B. | 3 | C. | -2 | D. | 2 |
3.以下长度的三条线段,不能组成三角形的是( )
| A. | 9、15、7 | B. | 4、9、6 | C. | 15、20、6 | D. | 3、8、4 |
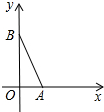 在平面直角坐标系中,点A(4,0)、B(0,8),以AB为斜边作等腰直角△ABC,则点C坐标为(6,6)和(-2,2).
在平面直角坐标系中,点A(4,0)、B(0,8),以AB为斜边作等腰直角△ABC,则点C坐标为(6,6)和(-2,2).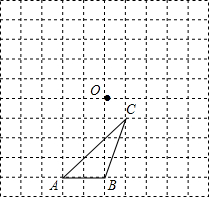 如图所示,△ABC与点O在10×10的网格中的位置如图所示
如图所示,△ABC与点O在10×10的网格中的位置如图所示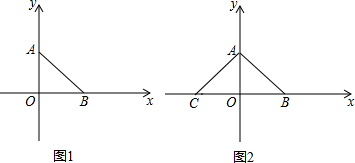
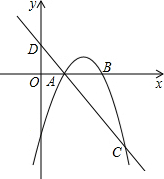 如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).
如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).