ЬтФПФкШн
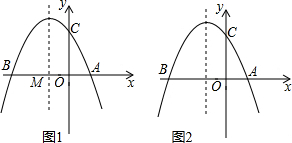
ШчЭМ1ЃЌХзЮяЯпy=ax2+bx+6ЃЈaЁй0ЃЉгыxжсНЛгкЕуAЃЈ2ЃЌ0ЃЉКЭЕуBЃЈ-6ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуMЃЌдкЖдГЦжсЩЯДцдкЕуPЃЌЪЙЁїCMPЮЊЕШбќШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЩшЕуQЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛИіЖЏЕуЃЌЕБЕуQТњзу|QB-QC|зюДѓЪБЃЌЧѓГіQЕуЕФзјБъЃЛ
ЃЈ4ЃЉШчЭМ2ЃЌШєЕуEЮЊЕкЖўЯѓЯоХзЮяЯпЩЯвЛЖЏЕуЃЌСЌНгBEЁЂCEЃЌЧѓЫФБпаЮBOCEЕФУцЛ§ЕФзюДѓжЕЃЌВЂЧѓДЫЪБEЕуЕФзјБъЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуMЃЌдкЖдГЦжсЩЯДцдкЕуPЃЌЪЙЁїCMPЮЊЕШбќШ§НЧаЮЃЌЧыжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЩшЕуQЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛИіЖЏЕуЃЌЕБЕуQТњзу|QB-QC|зюДѓЪБЃЌЧѓГіQЕуЕФзјБъЃЛ
ЃЈ4ЃЉШчЭМ2ЃЌШєЕуEЮЊЕкЖўЯѓЯоХзЮяЯпЩЯвЛЖЏЕуЃЌСЌНгBEЁЂCEЃЌЧѓЫФБпаЮBOCEЕФУцЛ§ЕФзюДѓжЕЃЌВЂЧѓДЫЪБEЕуЕФзјБъЃЎ

ПМЕуЃКЖўДЮКЏЪ§злКЯЬт
зЈЬтЃК
ЗжЮіЃКЃЈ1ЃЉНЋЕуAЃЈ2ЃЌ0ЃЉКЭЕуBЃЈ-6ЃЌ0ЃЉЗжБ№ДњШыy=ax2+bx+6ЃЌЕУЕНЙигкaЁЂbЕФЖўдЊвЛДЮЗНГЬзщЃЌНтЗНГЬзщЧѓГіaЁЂbЕФжЕЃЌНјЖјЕУЕНХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЃЈ1ЃЉЕФКЏЪ§НтЮіЪНЕУГіХзЮяЯпЕФЖдГЦжсЮЊx=-2ЃЌдйЧѓГіMЕуЕФзјБъЃЌгЩгкCЪЧХзЮяЯпгыyжсЕФНЛЕуЃЌвђДЫCЕФзјБъЮЊЃЈ0ЃЌ6ЃЉЃЌИљОнMЁЂCЕФзјБъЧѓГіCMЕФОрРыЃЎШЛКѓЗжШ§жжЧщПіНјааЬжТлЃКЂйCP=PMЃЛЂкCM=MPЃЛЂлCM=CPЃЛ
ЃЈ3ЃЉгЩХзЮяЯпЕФЖдГЦадПЩжЊQB=QAЃЌЙЪЕБQЁЂCЁЂAШ§ЕуЙВЯпЪБЃЌ|QB-QC|зюДѓЃЌСЌНсACВЂбгГЄЃЌНЛЖдГЦжсгкЕуQЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпACЕФНтЮіЪНЃЌдйНЋx=-2ДњШыЃЌЧѓГіyЕФжЕЃЌНјЖјЕУЕНQЕуЕФзјБъЃЛ
ЃЈ4ЃЉгЩгкЫФБпаЮBOCEВЛЪЧЙцдђЕФЫФБпаЮЃЌвђДЫПЩНЋЫФБпаЮBOCEЗжИюГЩЙцдђЕФЭМаЮНјааМЦЫуЃЌЙ§EзїEFЁЭxжсгкFЃЌЫФБпаЮBOCEЕФУцЛ§=Ш§НЧаЮBFEЕФУцЛ§+жБНЧЬнаЮFOCEЕФУцЛ§ЃЎжБНЧЬнаЮFOCEжаЃЌFOЮЊEЕФКсзјБъЕФОјЖджЕЃЌEFЮЊEЕФзнзјБъЃЌвбжЊCЕФзнзјБъЃЌОЭжЊЕРСЫOCЕФГЄЃЎдкШ§НЧаЮBFEжаЃЌBF=BO-OFЃЌвђДЫПЩгУEЕФКсзјБъБэЪОГіBFЕФГЄЃЎШчЙћИљОнХзЮяЯпЩшГіEЕФзјБъЃЌШЛКѓДњШыЩЯУцЕФЯпЖЮжаЃЌМДПЩЕУГіЙигкЫФБпаЮBOCEЕФУцЛ§гыEЕФКсзјБъЕФКЏЪ§ЙиЯЕЪНЃЌИљОнКЏЪ§ЕФаджЪМДПЩЧѓЕУЫФБпаЮBOCEЕФзюДѓжЕМАЖдгІЕФEЕФКсзјБъЕФжЕЃЎМДПЩЧѓГіДЫЪБEЕФзјБъЃЎ
ЃЈ2ЃЉИљОнЃЈ1ЃЉЕФКЏЪ§НтЮіЪНЕУГіХзЮяЯпЕФЖдГЦжсЮЊx=-2ЃЌдйЧѓГіMЕуЕФзјБъЃЌгЩгкCЪЧХзЮяЯпгыyжсЕФНЛЕуЃЌвђДЫCЕФзјБъЮЊЃЈ0ЃЌ6ЃЉЃЌИљОнMЁЂCЕФзјБъЧѓГіCMЕФОрРыЃЎШЛКѓЗжШ§жжЧщПіНјааЬжТлЃКЂйCP=PMЃЛЂкCM=MPЃЛЂлCM=CPЃЛ
ЃЈ3ЃЉгЩХзЮяЯпЕФЖдГЦадПЩжЊQB=QAЃЌЙЪЕБQЁЂCЁЂAШ§ЕуЙВЯпЪБЃЌ|QB-QC|зюДѓЃЌСЌНсACВЂбгГЄЃЌНЛЖдГЦжсгкЕуQЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпACЕФНтЮіЪНЃЌдйНЋx=-2ДњШыЃЌЧѓГіyЕФжЕЃЌНјЖјЕУЕНQЕуЕФзјБъЃЛ
ЃЈ4ЃЉгЩгкЫФБпаЮBOCEВЛЪЧЙцдђЕФЫФБпаЮЃЌвђДЫПЩНЋЫФБпаЮBOCEЗжИюГЩЙцдђЕФЭМаЮНјааМЦЫуЃЌЙ§EзїEFЁЭxжсгкFЃЌЫФБпаЮBOCEЕФУцЛ§=Ш§НЧаЮBFEЕФУцЛ§+жБНЧЬнаЮFOCEЕФУцЛ§ЃЎжБНЧЬнаЮFOCEжаЃЌFOЮЊEЕФКсзјБъЕФОјЖджЕЃЌEFЮЊEЕФзнзјБъЃЌвбжЊCЕФзнзјБъЃЌОЭжЊЕРСЫOCЕФГЄЃЎдкШ§НЧаЮBFEжаЃЌBF=BO-OFЃЌвђДЫПЩгУEЕФКсзјБъБэЪОГіBFЕФГЄЃЎШчЙћИљОнХзЮяЯпЩшГіEЕФзјБъЃЌШЛКѓДњШыЩЯУцЕФЯпЖЮжаЃЌМДПЩЕУГіЙигкЫФБпаЮBOCEЕФУцЛ§гыEЕФКсзјБъЕФКЏЪ§ЙиЯЕЪНЃЌИљОнКЏЪ§ЕФаджЪМДПЩЧѓЕУЫФБпаЮBOCEЕФзюДѓжЕМАЖдгІЕФEЕФКсзјБъЕФжЕЃЎМДПЩЧѓГіДЫЪБEЕФзјБъЃЎ
НтД№ЃКНтЃКЃЈ1ЃЉгЩЬтжЊЃК
ЃЌ
НтЕУЃК
ЃЌ
ЙЪЫљЧѓХзЮяЯпНтЮіЪНЮЊЃКy=-
x2-2x+6ЃЛ
ЃЈ2ЃЉЁпХзЮяЯпНтЮіЪНЮЊЃКy=-
x2-2x+6ЃЌ
ЁрЖдГЦжсЮЊx=
=-2ЃЌ
ЩшPЕузјБъЮЊЃЈ-2ЃЌtЃЉЃЌ
ЁпЕБx=0ЪБЃЌy=6ЃЌ
ЁрCЃЈ0ЃЌ6ЃЉЃЌMЃЈ-2ЃЌ0ЃЉЃЌ
ЁрCM2=ЃЈ-2-0ЃЉ2+ЃЈ0-6ЃЉ2=40ЃЎ
ЂйЕБCP=PMЪБЃЌЃЈ-2ЃЉ2+ЃЈt-6ЃЉ2=t2ЃЌНтЕУt=
ЃЌ
ЁрPЕузјБъЮЊЃКP1ЃЈ-2ЃЌ
ЃЉЃЛ
ЂкЕБCM=PMЪБЃЌ40=t2ЃЌНтЕУt=ЁР2
ЃЌ
ЁрPЕузјБъЮЊЃКP2ЃЈ-2ЃЌ2
ЃЉЛђP3ЃЈ-2ЃЌ-2
ЃЉЃЛ
ЂлЕБCM=CPЪБЃЌгЩЙДЙЩЖЈРэЕУЃК40=ЃЈ-2ЃЉ2+ЃЈt-6ЃЉ2ЃЌНтЕУt=12ЃЌ
ЁрPЕузјБъЮЊЃКP4ЃЈ-2ЃЌ12ЃЉЃЎ
злЩЯЫљЪіЃЌДцдкЗћКЯЬѕМўЕФЕуPЃЌЦфзјБъЮЊPЃЈ-2ЃЌ
ЃЉЛђPЃЈ-2ЃЌ2
ЃЉЛђPЃЈ-2ЃЌ-2
ЃЉЛђPЃЈ-2ЃЌ12ЃЉЃЛ
ЃЈ3ЃЉЁпЕуAЃЈ2ЃЌ0ЃЉКЭЕуBЃЈ-6ЃЌ0ЃЉЙигкХзЮяЯпЕФЖдГЦжсx=-2ЖдГЦЃЌ
ЁрQB=QAЃЌ
Ёр|QB-QC|=|QA-QC|ЃЌ
вЊЪЙ|QB-QC|зюДѓЃЌдђСЌНсACВЂбгГЄЃЌгыжБЯпx=-2ЯрНЛгкЕуQЃЌМДЕуQЮЊжБЯпACгыжБЯпx=-2ЕФНЛЕуЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊy=kx+mЃЌ
ЁпAЃЈ2ЃЌ0ЃЉЃЌCЃЈ0ЃЌ6ЃЉЃЌ
Ёр
ЃЌ
НтЕУ
ЃЌ
Ёрy=-3x+6ЃЌ
ЕБx=-2ЪБЃЌy=-3ЁСЃЈ-2ЃЉ+6=12ЃЌ
ЙЪЕБQдкЃЈ-2ЃЌ12ЃЉЕФЮЛжУЪБЃЌ|QB-QC|зюДѓЃЛ
 ЃЈ4ЃЉЙ§ЕуEзїEFЁЭxжсгкЕуFЃЌЩшEЃЈnЃЌ-
ЃЈ4ЃЉЙ§ЕуEзїEFЁЭxжсгкЕуFЃЌЩшEЃЈnЃЌ-
n2-2n+6ЃЉЃЈ-6ЃМnЃМ0ЃЉЃЌ
дђEF=-
n2-2n+6ЃЌBF=n+6ЃЌOF=-nЃЌ
SЫФБпаЮBOCE=
BF•EF+
ЃЈOC+EFЃЉ•OF
=
ЃЈn+6ЃЉ•ЃЈ-
n2-2n+6ЃЉ+
ЃЈ6-
n2-2n+6ЃЉ•ЃЈ-nЃЉ
=-
n2-9n+18=-
ЃЈn+3ЃЉ2+
ЃЌ
ЫљвдЕБn=-3ЪБЃЌSЫФБпаЮBOCEзюДѓЃЌЧвзюДѓжЕЮЊ
ЃЎ
ДЫЪБЃЌЕуEзјБъЮЊЃЈ-3ЃЌ
ЃЉЃЎ
|
НтЕУЃК
|
ЙЪЫљЧѓХзЮяЯпНтЮіЪНЮЊЃКy=-
| 1 |
| 2 |
ЃЈ2ЃЉЁпХзЮяЯпНтЮіЪНЮЊЃКy=-
| 1 |
| 2 |
ЁрЖдГЦжсЮЊx=
| 2 | ||
2ЁС(-
|
ЩшPЕузјБъЮЊЃЈ-2ЃЌtЃЉЃЌ
ЁпЕБx=0ЪБЃЌy=6ЃЌ
ЁрCЃЈ0ЃЌ6ЃЉЃЌMЃЈ-2ЃЌ0ЃЉЃЌ
ЁрCM2=ЃЈ-2-0ЃЉ2+ЃЈ0-6ЃЉ2=40ЃЎ
ЂйЕБCP=PMЪБЃЌЃЈ-2ЃЉ2+ЃЈt-6ЃЉ2=t2ЃЌНтЕУt=
| 10 |
| 3 |
ЁрPЕузјБъЮЊЃКP1ЃЈ-2ЃЌ
| 10 |
| 3 |
ЂкЕБCM=PMЪБЃЌ40=t2ЃЌНтЕУt=ЁР2
| 10 |
ЁрPЕузјБъЮЊЃКP2ЃЈ-2ЃЌ2
| 10 |
| 10 |
ЂлЕБCM=CPЪБЃЌгЩЙДЙЩЖЈРэЕУЃК40=ЃЈ-2ЃЉ2+ЃЈt-6ЃЉ2ЃЌНтЕУt=12ЃЌ
ЁрPЕузјБъЮЊЃКP4ЃЈ-2ЃЌ12ЃЉЃЎ
злЩЯЫљЪіЃЌДцдкЗћКЯЬѕМўЕФЕуPЃЌЦфзјБъЮЊPЃЈ-2ЃЌ
| 10 |
| 3 |
| 10 |
| 10 |
ЃЈ3ЃЉЁпЕуAЃЈ2ЃЌ0ЃЉКЭЕуBЃЈ-6ЃЌ0ЃЉЙигкХзЮяЯпЕФЖдГЦжсx=-2ЖдГЦЃЌ
ЁрQB=QAЃЌ
Ёр|QB-QC|=|QA-QC|ЃЌ
вЊЪЙ|QB-QC|зюДѓЃЌдђСЌНсACВЂбгГЄЃЌгыжБЯпx=-2ЯрНЛгкЕуQЃЌМДЕуQЮЊжБЯпACгыжБЯпx=-2ЕФНЛЕуЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊy=kx+mЃЌ
ЁпAЃЈ2ЃЌ0ЃЉЃЌCЃЈ0ЃЌ6ЃЉЃЌ
Ёр
|
НтЕУ
|
Ёрy=-3x+6ЃЌ
ЕБx=-2ЪБЃЌy=-3ЁСЃЈ-2ЃЉ+6=12ЃЌ
ЙЪЕБQдкЃЈ-2ЃЌ12ЃЉЕФЮЛжУЪБЃЌ|QB-QC|зюДѓЃЛ
 ЃЈ4ЃЉЙ§ЕуEзїEFЁЭxжсгкЕуFЃЌЩшEЃЈnЃЌ-
ЃЈ4ЃЉЙ§ЕуEзїEFЁЭxжсгкЕуFЃЌЩшEЃЈnЃЌ-| 1 |
| 2 |
дђEF=-
| 1 |
| 2 |
SЫФБпаЮBOCE=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 63 |
| 2 |
ЫљвдЕБn=-3ЪБЃЌSЫФБпаЮBOCEзюДѓЃЌЧвзюДѓжЕЮЊ
| 63 |
| 2 |
ДЫЪБЃЌЕуEзјБъЮЊЃЈ-3ЃЌ
| 15 |
| 2 |
ЕуЦРЃКБОЬтЪЧЖўДЮКЏЪ§ЕФзлКЯЬтаЭЃЌЦфжаЩцМАЕНЕФжЊЪЖЕугаД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§ЁЂвЛДЮКЏЪ§ЕФНтЮіЪНЃЌЕШбќШ§НЧаЮЕФаджЪЃЌЖўДЮКЏЪ§ЕФаджЪЃЌЫФБпаЮЕФУцЛ§ЃЌзлКЯадНЯЧПЃЌФбЖШЪЪжаЃЎРћгУЪ§аЮНсКЯЁЂЗжРрЬжТлМАЗНГЬЫМЯыЪЧНтЬтЕФЙиМќЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
Дг2009Фъ1дТ1ШеЦ№ЃЌжиЧьЪаНЋЗПВњНЛвзЦѕЫАЃЌгЩдРДЕФ1%НЕЕЭЕН0.5%ЃЎБОМОЖШЗПВњНЛвзЦѕЫАЮЊ104040000дЊЃЌгУПЦбЇМЧЪ§ЗЈБэЪОЮЊЃЈЁЁЁЁЃЉ
| AЁЂ10.404ЁС108дЊ |
| BЁЂ0.10404ЁС108дЊ |
| CЁЂ1.0404ЁС109дЊ |
| DЁЂ1.0404ЁС108дЊ |
 ШчЭМЃЌаЁУїЪщЩЯЕФШ§НЧаЮБЛФЋМЃЮлШОСЫвЛВПЗжЃЌЫћИљОнЫљбЇжЊЪЖЛГівЛИігыДЫШ§НЧаЮШЋЕШЕФШ§НЧаЮЃЌЫћЛЭМвРОнЕФЛљБОЪТЪЕЪЧ
ШчЭМЃЌаЁУїЪщЩЯЕФШ§НЧаЮБЛФЋМЃЮлШОСЫвЛВПЗжЃЌЫћИљОнЫљбЇжЊЪЖЛГівЛИігыДЫШ§НЧаЮШЋЕШЕФШ§НЧаЮЃЌЫћЛЭМвРОнЕФЛљБОЪТЪЕЪЧ ШчЭМЃЌDEЁЮBCЃЎ
ШчЭМЃЌDEЁЮBCЃЎ ШчЭМЫљЪОЃЌABЁЮCDЁЮEFЃЌAFгыBEЯрНЛгкЕуGЃЌЧвAG=2ЃЌGD=1ЃЌDF=5ЃЌЧѓ
ШчЭМЫљЪОЃЌABЁЮCDЁЮEFЃЌAFгыBEЯрНЛгкЕуGЃЌЧвAG=2ЃЌGD=1ЃЌDF=5ЃЌЧѓ