题目内容
 如图,小明书上的三角形被墨迹污染了一部分,他根据所学知识画出一个与此三角形全等的三角形,他画图依据的基本事实是
如图,小明书上的三角形被墨迹污染了一部分,他根据所学知识画出一个与此三角形全等的三角形,他画图依据的基本事实是考点:全等三角形的应用
专题:
分析:根据全等三角形的判定方法解答即可.
解答:解:依据为:两角及其夹边分别相等的两个三角形全等(ASA).
故答案为:两角及其夹边分别相等的两个三角形全等.
故答案为:两角及其夹边分别相等的两个三角形全等.
点评:本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
相关题目
用配方法解一元二次方程x2+6x-16=0,配方后的方程为( )
| A、(x+3)2=25 |
| B、(x-3)2=25 |
| C、(x+3)2=16 |
| D、(x+9)2=25 |
要使分式
有意义,则( )
| 1 |
| 3+x |
| A、x>-3 | B、x<-3 |
| C、x≠3 | D、x≠-3 |
已知:线段AB:A(2,-4),B(3,1)在平面直角坐标系中平移,A到A′(-1,1),则B点移到B′的坐标为( )
| A、(0,-4) |
| B、(6,6) |
| C、(0,6) |
| D、(6,-9) |
下列各数中,互为相反数的是( )
| A、-3与-|-3| |
| B、(-3)2与32 |
| C、-(-25)与-52 |
| D、-6与(-2)×3 |
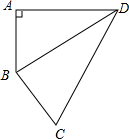 如图,四边形ABCD中,∠A=90.,连结对角线BD,BD⊥BC,现测得:AB=9cm,AD=12cm,CD=17cm,求四边形ABCD的面积.
如图,四边形ABCD中,∠A=90.,连结对角线BD,BD⊥BC,现测得:AB=9cm,AD=12cm,CD=17cm,求四边形ABCD的面积.
 在四边形ABCD中,∠ABC=90°,AB=BC=4,CD=2,AD=6,求∠BCD的度数.
在四边形ABCD中,∠ABC=90°,AB=BC=4,CD=2,AD=6,求∠BCD的度数.