题目内容
在△ABC中,AB=15cm,BC=20cm,AC=30cm,另一个与它相似的△A′B′C′的最短边长为45cm,则△A′B′C′的周长为 .
考点:相似三角形的性质
专题:
分析:利用最短边可求得两三角形的相似比,且可求得△ABC的周长,再根据周长比等于相似比可求得△A′B′C′的周长.
解答:解:
∵△ABC∽△A′B′C′,且△ABC中最短边为15cm,△A′B′C′的最短边长为45cm,
∴相似比为
=
,
∴
=
,
又△ABC的周长为15+20+30=65(cm),
∴
=
,
解得C△A′B′C′=195cm,
故答案为:195cm.
∵△ABC∽△A′B′C′,且△ABC中最短边为15cm,△A′B′C′的最短边长为45cm,
∴相似比为
| 15 |
| 45 |
| 1 |
| 3 |
∴
| C△ABC |
| C△A′B′C′ |
| 1 |
| 3 |
又△ABC的周长为15+20+30=65(cm),
∴
| 65 |
| C△A′B′C′ |
| 1 |
| 3 |
解得C△A′B′C′=195cm,
故答案为:195cm.
点评:本题主要考查相似三角形的性质,掌握相似三角形的周长比等于相似比是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若半径为1和5的两圆外离,则圆心距d的取值范围为( )
| A、d>6 | B、4<d<6 |
| C、d=6 | D、d=4 |
用配方法解一元二次方程x2+6x-16=0,配方后的方程为( )
| A、(x+3)2=25 |
| B、(x-3)2=25 |
| C、(x+3)2=16 |
| D、(x+9)2=25 |
A、B两地相距s千米,甲、乙两人分别以45千米/小时、40千米/小时的速度从A到B,若甲先走1小时,则甲比乙早到的时间为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
菱形的周长为16,且有一个内角为120°,则此菱形的面积为( )
A、4
| ||
B、8
| ||
C、10
| ||
D、12
|
下列大学的校徽图案是轴对称图形的是( )
A、 清华大学 |
B、 北京大学 |
C、 中国人民大学 |
D、 浙江大学 |
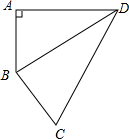 如图,四边形ABCD中,∠A=90.,连结对角线BD,BD⊥BC,现测得:AB=9cm,AD=12cm,CD=17cm,求四边形ABCD的面积.
如图,四边形ABCD中,∠A=90.,连结对角线BD,BD⊥BC,现测得:AB=9cm,AD=12cm,CD=17cm,求四边形ABCD的面积.