题目内容
4.先阅读后解题:若m2+2m+n2-6n+10=0,求m和n的值.
解:等式可变形为:m2+2m+1+n2-6n+9=0
即 (m+1)2+(n-3)2=0
因为(m+1)2≥0,(n-3)2≥0,
所以 m+1=0,n-3=0
即 m=-1,n=3.
像这样将代数式进行恒等变形,使代数式中出现完全平方式的方法叫做“配方法”.请利用配方法,解决下列问题:
(1)已知x2+y2+x-6y+$\frac{37}{4}$=0,求xy的值;
(2)已知△ABC的三边长a、b、c都是正整数,且满足2a2+b2-4a-6b+11=0,则△ABC的周长是7;
(3)a2+b2+4a-10b+30的最小值是1.
分析 (1)根据配方法,可得x,y的值,根据乘方的意义,可得答案;
(2)根据配方法,可得a,b的值,在根据三角形三边的关系,可得c的值,根据三角形的周长,可得答案;
(3)根据配方法,可得非负数的和,根据非负数的性质,可得答案.
解答 解:(1)等式可变形为:x2+x+$\frac{1}{4}$+y2-6y+9=0,
即(x+$\frac{1}{2}$)2+(y-3)2=0
∵(x+$\frac{1}{2}$)2≥0,(y-3)2≥0,
∴x+$\frac{1}{2}$=0,y-3=0,
即x=-$\frac{1}{2}$,y=3.
xy=(-$\frac{1}{2}$)3=-$\frac{1}{8}$;
(2)等式可变形为($\sqrt{2}$a)2-4a+($\sqrt{2}$)2+b2-6b+9=0,
即($\sqrt{2}$a-$\sqrt{2}$)2+(b-3)2=0,
∵($\sqrt{2}$a-$\sqrt{2}$)2≥0,(b-3)2≥0,
∴$\sqrt{2}$a-$\sqrt{2}$=0,b-3=0,
即a=1,b=3,
由三角形三边的关系,得
2<c<4,
又∵a、b、c都是正整数,
∴c=3,
△ABC的周长是3+3+1=7;
(3)原式=a2-4a+4+b2-10b+25+1
=(a-2)2+(b-5)2+1
∵(a-2)2≥0,(b-5)2≥0,
∴a2+b2+4a-10b+30的最小值是1,
故答案为:7,1.
点评 本题考查了非负数的性质,利用配方法得出非负数的和是解题关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
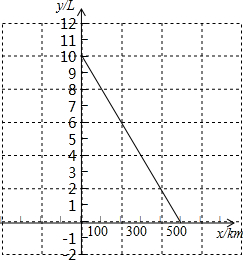 某种摩托车的油箱加油满后,油箱中的剩余油量y(L)与摩托车行驶路程x(km)之间的关系如图所示.根据图象回答下列问题:
某种摩托车的油箱加油满后,油箱中的剩余油量y(L)与摩托车行驶路程x(km)之间的关系如图所示.根据图象回答下列问题: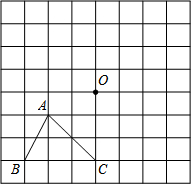 如图,在方格网中已知格点△ABC和点O.
如图,在方格网中已知格点△ABC和点O.