Question

12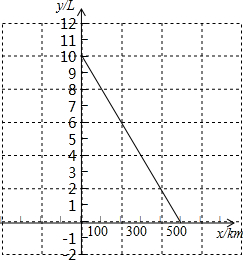．某种摩托车的油箱加油满后，油箱中的剩余油量y（L）与摩托车行驶路程x（km）之间的关系如图所示．根据图象回答下列问题：
（1）油箱最多可储油多少升？
（2）一箱汽油可供摩托车行驶多少千米？
（3）写出剩余油量y（L）与行驶路程x（km）之间的关系式．
（4）油箱中的剩余油量小于1L时，摩托车将自动报警．行驶多少千米后，摩托车将自动报警？

Answer 1

分析 （1）观察函数图象，找出当x=0时，y的值即可；
（2）观察函数图象，找出当y=0时，x的值即可；
（3）根据函数图象上点的坐标利用待定系数法求出一次函数关系式是解题的关键；
（4）将y=1代入一次函数关系式中求出x值即可．

解答 解：（1）∵当x=0时，y=10，
∴油箱最多可储油10升．

（2）∵当y=0时，x=500，
∴一箱汽油可供摩托车行驶500千米．

（3）设剩余油量y（L）与行驶路程x（km）之间的关系式为y=kx+b（k≠0），
将（0，10）、（500，0）代入y=kx+b，
$\left\{\begin{array}{l}{b=10}\\{500k+b=0}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=-\frac{1}{50}}\\{b=10}\end{array}\right.$，
∴剩余油量y（L）与行驶路程x（km）之间的关系式为y=-$\frac{1}{50}$x+10（0≤x≤500）．
（4）当y=1时，有-$\frac{1}{50}$x+10=1，
解得：x=450．
答：行驶450千米后，摩托车将自动报警．

点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征，解题的关键是：（1）找出当x=0时y的值；（2）找出y=0时x的值；（3）根据点的坐标利用待定系数法求出一次函数关系式；（4）求出当y=1时x的值．