��Ŀ����
2�� ��֪������������y=ax��a��0����ͼ���뷴��������y=$\frac{k}{x}$��k��0����ͼ���ڵ㣨2��2$\sqrt{2}$+2��
��֪������������y=ax��a��0����ͼ���뷴��������y=$\frac{k}{x}$��k��0����ͼ���ڵ㣨2��2$\sqrt{2}$+2����1����ȷ�����������������ͷ����������ı���ʽ��
��2����һ�����ڣ�������������y=$\frac{k}{x}$��ֵ��������������y=ax��ֵʱ����x��ȡֵ��Χ��
��3����ͼ��M��m��n����A��n��m���ڵ�һ������Ϊ����������ͼ���ϵ������㣬����M��ֱ��MB��x�ᣬ��y���ڵ�B������A��ֱ��AC��y�ύx���ڵ�C����ֱ��MB�ڵ�D������MOA=45��ʱ����M�����꣮
���� ��1�����㣨2��2$\sqrt{2}$+2������������������ʽ���ɣ�
��2���۲���������ͼ���λ�ã�����������ͼ�������棬����д���𰸣�
��3������OMB�Ƶ�O˳ʱ����ת90��õ���OCE������AM��ֻҪ֤��AM=BM+AC���г�����m��n�ķ��̼��ɽ����
��� �⣺��1���ѵ㣨2��2$\sqrt{2}$+2���ֱ���������������ͷ�������������ʽ�ã�
2$\sqrt{2}$+2=2a�����a=$\sqrt{2}$+1��2$\sqrt{2}$+2=$\frac{k}{2}$�����k=4$\sqrt{2}$+4��
������������������ʽΪ��y=��$\sqrt{2}$+1��x��
��������������ʽ��y=$\frac{4\sqrt{2}+4}{x}$��
��2����0��x��2ʱ������������y=$\frac{k}{x}$��ֵ��������������y=ax��ֵ��
��3����ΪM��n��m����A��m��n������֪���ı���BOCDΪ�����Σ��֡�MOA=45�㣬
����OMB�Ƶ�O˳ʱ����ת90��õ���OCE������AM��
�ߡ�BOM+��AOC=45�㣬��BOM=��EOC��OE=OM��BM=CE��
���AOC+��EOC=45��=��MOA��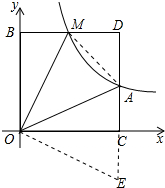
�ڡ�OAM�͡�OAE�У�
$\left\{\begin{array}{l}{OA=OA}\\{��AOM=��AOE}\\{OOE}\end{array}\right.$��
���OAM�ա�OAE��
��AM=AE=AC+CE=AC+BM
�֡�BM=m��AC=m��
��AM=2m��MD=n-m=DA��
��������MDA�ǵ��������Σ�MA=$\sqrt{2}$MD��2m=$\sqrt{2}$��n-m�� �٣�
�֡�M���ڷ���������ͼ���ϣ�
��mn=4$\sqrt{2}$+4 �ڣ�
�ɢ٢ڽ��$\left\{\begin{array}{l}{m=2}\\{n=2\sqrt{2}+2}\end{array}\right.$��
��M��2��2$\sqrt{2}$+2����
���� ���⿼�鷴����������һ�κ�����ͼ��Ľ��㣬ѧ�����ϵ������������ʽ���ܸ���ͼ���ɺ���ֵ�Ĵ�Сȷ���Ա�����ȡֵ��Χ���������������Ӹ������ǽ������Ĺؼ��������п��������ͣ�

| A�� | 38 | B�� | 39 | C�� | 40 | D�� | 42 |
| A�� | $\frac{3}{28}$ | B�� | $\frac{5}{28}$ | C�� | $\frac{3}{56}$ | D�� | $\frac{5}{56}$ |
 ��ͼ��ֱ��CD���B��һ���ཻ�ڵ�E����CD��AB������BED=70�㣬���B�Ķ�������70�㣮
��ͼ��ֱ��CD���B��һ���ཻ�ڵ�E����CD��AB������BED=70�㣬���B�Ķ�������70�㣮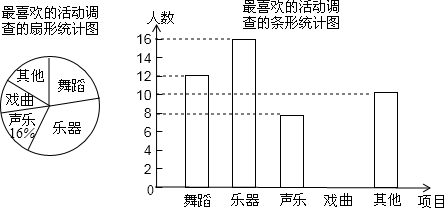
 ��ͼ����֪���ı���ABCD�У�AE��BD��EE��CF��BD��F��AE=CF��BF=DE����֤���ı���ABCD��ƽ���ı��Σ�
��ͼ����֪���ı���ABCD�У�AE��BD��EE��CF��BD��F��AE=CF��BF=DE����֤���ı���ABCD��ƽ���ı��Σ�