题目内容
 如图,在△ABC中,∠ABC=45°,高线AD和BE交于点F.求证:CD=DF.
如图,在△ABC中,∠ABC=45°,高线AD和BE交于点F.求证:CD=DF.考点:全等三角形的判定与性质
专题:证明题
分析:由AD与BE为两条高,得到一对直角相等,再由一对对顶角相等,利用内角和定理得到∠CAD=∠FBD,根据∠ABC=45°,得到三角形ABD为等腰直角三角形,即AD=BD,利用ASA得到三角形ADC与三角形BDF全等,利用全等三角形的对应边相等即可得证.
解答:证明:∵AD、BE是△ABC的高线,
∴AD⊥BC,BE⊥AC,
∴∠ADB=∠ADC=90°,∠AEB=90°,
∵∠ABC=45°,
∴△ADB是等腰直角三角形,
∴AD=BD,
∵∠EBC+∠BFD=90°,∠CAD+∠AFE=90°,∠AFE=∠BFD,
∴∠CAD=∠EBC,
在△BDF和△ADC中,
,
∴△BDF≌△ADC(ASA),
∴CD=DF.
∴AD⊥BC,BE⊥AC,
∴∠ADB=∠ADC=90°,∠AEB=90°,
∵∠ABC=45°,
∴△ADB是等腰直角三角形,
∴AD=BD,
∵∠EBC+∠BFD=90°,∠CAD+∠AFE=90°,∠AFE=∠BFD,
∴∠CAD=∠EBC,
在△BDF和△ADC中,
|
∴△BDF≌△ADC(ASA),
∴CD=DF.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
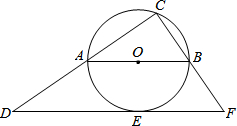 如图,AB为⊙O的直径,C为⊙O上一点,DF切⊙O于E点,分别与CA、CB的延长线于点D、F,已知AB∥DF,CD=4,CF=3,则AC=( )
如图,AB为⊙O的直径,C为⊙O上一点,DF切⊙O于E点,分别与CA、CB的延长线于点D、F,已知AB∥DF,CD=4,CF=3,则AC=( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知不等式组
,则化简|4x+5|-|x-1|的结果为( )
|
| A、3x+4 | B、3x+6 |
| C、5x+4 | D、5x+6 |
 如图,在Rt△ABC中,∠A=90°,点O在AC上,⊙O切BC于点E,A在⊙O上,若AB=5,AC=12,求⊙O的半径.
如图,在Rt△ABC中,∠A=90°,点O在AC上,⊙O切BC于点E,A在⊙O上,若AB=5,AC=12,求⊙O的半径. 已知关于x一元二次方程x2-2(k+1)x+k2-2k-3=0有两个不相等的实数根
已知关于x一元二次方程x2-2(k+1)x+k2-2k-3=0有两个不相等的实数根